
Tọa độ giao điểm của hai đường thẳng \({d_1}:y = \frac{{1 - 3x}}{4}\) và \({d_2}:y = - \left( {\frac{x}{3} + 1} \right)\) là:A. \(\left( {0; - 1} \right)\)B. \(\left( { - \frac{7}{3};2} \right)\)C. \(\left( {0;\frac{1}{4}} \right)\)D. \(\left( {3; - 2} \right)\)

Vẽ đồ thị hàm số của cả 2 đường thẳng sau đó xác định tọa độ giao điểm.

Ta có: \({d_1}:y = \frac{{1 - 3x}}{4} = - \frac{3}{4}x + \frac{1}{4}\)
\({d_2}:y = - \left( {\frac{x}{3} + 1} \right) = - \frac{1}{3}x - 1\)
Xét đồ thị hàm số \({d_1}:y = \frac{{ - 3}}{4}x + \frac{1}{4}\)
Chọn \(x = 0\) suy ra \(y = \frac{1}{4}\)
Chọn \(y = 0\) suy ra \(x = \frac{1}{3}\)
Advertisements (Quảng cáo)
Vậy đồ thị hàm số \({d_1}:y = \frac{{ - 3}}{4}x + \frac{1}{4}\) là đường thẳng đi qua hai điểm \(A\left( {0;\frac{1}{4}} \right),B\left( {\frac{1}{3};0} \right)\)
Xét đồ thị hàm số \({d_2}:y = - \frac{1}{3}x - 1\)
Chọn \(x = 0\) suy ra \(y = - 1\)
Chọn \(y = 0\) suy ra \(x = - 3\)
Vậy đồ thị hàm số \({d_2}:y = - \frac{1}{3}x - 1\) là đường thẳng đi qua hai điểm \(C\left( {0; - 1} \right),D\left( { - 3;0} \right)\)
Vẽ trên mặt phẳng tọa độ \(Oxy\):
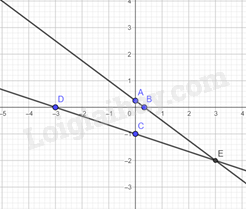
Ta xác định được giao điểm \(E\left( {3; - 2} \right)\).
→ Đáp án D.
