Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
Giải:
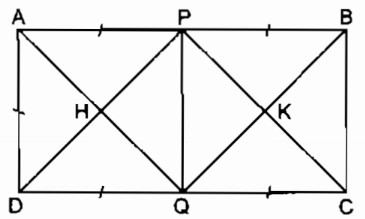
Xét tứ giác APQD ta có:
AB // CD (gt) hay AP // QD
AP = \({1 \over 2}\)AB (gt)
QD = \({1 \over 2}\)CD (gt)
Suy ra: AP = QD nên tứ giác APQD là hình bình hành.
\(\widehat A = {90^0}\)
Suy ra: Tứ giác APQD là hình chữ nhật
AD = AP = \({1 \over 2}\)AB
Vậy : Tứ giác APQD là hình vuông
⇒ AQ ⊥ PD (tính chất hình vuông) \( \Rightarrow \widehat {PHQ} = {90^0}\) (1)
HP = HQ (tính chất hình vuông)
Advertisements (Quảng cáo)
- Xét tứ giác PBCQ ta có:
PB // CD
PB = \({1 \over 2}\)AB (gt)
CQ = \({1 \over 2}\)CD (gt)
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
\(\widehat B = {90^0}\)suy ra tứ giác PBCQ là hình chữ nhật
PB = BC (vì cùng bằng AD = \({1 \over 2}\)AB)
Vậy: Tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (tính chất hình vuông) \( \Rightarrow \widehat {PKQ} = {90^0}\)(2)
PD là tia phân giác \(\widehat {APQ}\) (tính chất hình vuông)
PC là tia phân giác \(\widehat {QPB}\) (tính chất hình vuông)
Suy ra: PD ⊥ PC (tính chất hai góc kề bù) ⇒ \(\widehat {HPK} = {90^0}\) (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
