Cho tam giác ABC . Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E.
a. Tìm các hình thang trong hình vẽ
b. Chứng minh rằng hình thang BDEC có một cạnh đáy bằng tổng hai cạnh bên.
Giải:
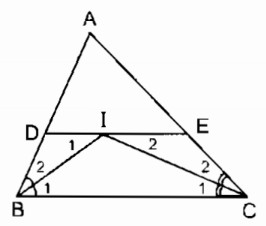
a. Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC.
b. DE // BC (theo cách vẽ)
\( \Rightarrow {\widehat I_1} = {\widehat B_1}\) (hai góc so le trong)
Mà \({\widehat B_1} = {\widehat B_2}\) (gt)
Advertisements (Quảng cáo)
Suy ra: \({\widehat I_1} = {\widehat B_2}\)
Do đó: ∆ BDI cân tại D
⇒ DI = DB (1)
Ta có: \({\widehat I_2} = {\widehat C_1}\) (so le trong)
\({\widehat C_1} = {\widehat C_2}\) (gt)
Suy ra: \({\widehat I_2} = {\widehat C_2}\) do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2) và (3) suy ra: DE = BD + CE
