Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE // IK, DE = IK.. Câu 38 trang 84 Sách bài tập (SBT) Toán 8 tập 1 - Bài 4. Đường trung bình của tam giác của hình thang
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE // IK, DE = IK.
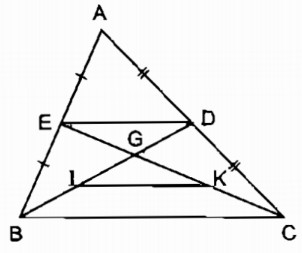
Trong tam giác ABC ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của tam giác ABC
Advertisements (Quảng cáo)
⇒ED // BC và \(ED = {{BC} \over 2}\) (tính chất đường trung bình của tam giác) (1)
Trong tam giác GBC ta có:
I là trung điểm của BG (gt)
K là trung điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và \(IK = {{BC} \over 2}\) (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: IK // DE và IK = DE.