Dựng tứ giác ABCD, biết AB = 2cm, AD = 3cm . Câu 58 trang 86 Sách bài tập (SBT) Toán 8 tập 1 - Bài 5. Dựng hình bằng thước và com pa. Dựng hình thang
Dựng tứ giác ABCD, biết AB = 2cm, AD = 3cm, \(\widehat A = {80^0},\widehat B = {120^0},\widehat C = {100^0}\).
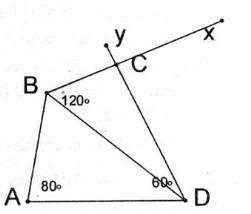
Cách dựng:
- Dựng ∆ ABD biết AB = 2cm, \(\widehat A = {80^0}\), AD = 3cm.
Advertisements (Quảng cáo)
- Dựng \(\widehat {ABx} = {120^0}\)
- Trên nửa mặt phẳng bờ AD chứa đỉnh D dựng \(\widehat {ADy} = {60^0}\). Dy cắt Bx tại C.
Chứng minh: Thật vậy theo cách dựng AB = 2cm, \(\widehat A = {80^0}\), AD = 3cm, \(\widehat B = {120^0}\)
\(\eqalign{
& \widehat C = {360^0} - \left( {\widehat A + \widehat B + \widehat D} \right) \cr
& = {360^0} - \left( {{{80}^0} + {{120}^0} + {{60}^0}} \right) = {100^0} \cr} \)
Tứ giác ABCD dựng được thỏa mãn điều kiện bài toán.