
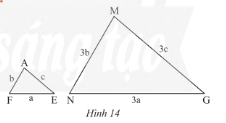
a) Tam giác \(AFE\) và \(MNG\) ở Hình 14 có đồng dạng với nhau không? Vì sao?
b) Biết tam giác \(AFE\) có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Nếu tam giác \(ABC\) đồng dạng với tam giác \(A’B’C’\) theo tỉ số \(k\) thì tỉ số chu vi của hai tam giác đó cũng bằng \(k\).

a) Ta có:
Advertisements (Quảng cáo)
\(\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}\)
Xét tam giác \(AFE\) và tam giác \(MNG\) có:
\(\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}\)
Do đó, \(\Delta AFE\backsim\Delta MNG\) (c.c.c)
b) Tỉ số đồng dạng của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\).
Do đó, tỉ số chu vi của của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\) (tính chất)
Do đó, chu vi tam giác \(MNG\) là: \(15.3 = 45cm\)
Vậy chu vi tam giác \(MNG\) là 45 cm.
