Bài 2 trang 76 Toán 8 tập 2– Chân trời sáng tạo: Quan sát Hình 9. Chứng minh rằng \(\Delta DEF\backsim\Delta HDF\). Chứng minh rằng \(D{F^2} = FH. FE\)...

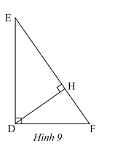
Quan sát Hình 9.

a) Chứng minh rằng \(\Delta DEF\backsim\Delta HDF\).

b) Chứng minh rằng \(D{F^2} = FH.FE\).

c) Biết \(EF = 15cm,FH = 5,4cm\). Tính độ dài đoạn thẳng \(DF\).

Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:

\(\widehat F\) chung

\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)

Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)

b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

\( \Rightarrow D{F^2} = FH.FE\).

c) Theo câu b ta có:

\(D{F^2} = FH.FE\)

Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)

Vậy \(DF = 9cm\).