Hoạt động 1
Dùng thước đo góc để đo số đo các góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) ở Hình 1 và rút ra nhận xét và số đo của chúng.


Dùng thước đo góc để đo số đo 4 góc của tứ giác rồi rút ra nhận xét.

Sau khi đo, ta thấy bốn góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) có số đo bằng nhau và bằng \(90^\circ \)
Hoạt động 2
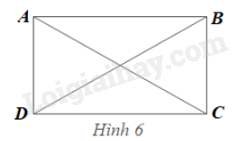
Cho \(ABCD\) là hình chữ nhật.
a) Chứng minh \(AB\) // \(CD\) và \(AD\) // \(BC\)
b) Tam giác \(ABD\) và tam giác \(BAC\) có bằng nhau không? Vì sao?

Áp dụng các tính chất của hình chữ nhật (cạnh, góc)

a) Vì \(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\), \(\widehat {DAB} = \widehat {ABC} = \widehat {DCB} = \widehat {ADC} = 90^\circ \)
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ADC}}}\) (cmt)
\(BC = AD\) (gt)
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) và \(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (hai cạnh tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\); \(BC\) // \(AD\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(AB\) chung
\(\widehat {{\rm{BAD}}} = \widehat {{\rm{ABC}}}\) (cmt)
\(AD = BC\) (cmt)
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Thực hành 1
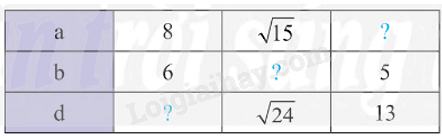
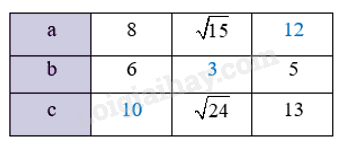
Cho biết \(a\), \(b\), \(d\) lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.


Áp dụng định lý Pythagore trong tam giác vuông

Giả sử \(ABCD\) là hình chữ nhật ; \(a\), \(b\), \(d\) lần lượt là độ dài của \(AB\), \(BC\), \(AC\)
Áp dụng định lý Pythagore vào \(\Delta ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Do đó \({d^2} = {a^2} + {b^2}\) ; \({b^2} = {d^2} - {a^2}\); \({a^2} = {d^2} - {b^2}\)
Suy ra: \(d = \sqrt {{a^2} + {b^2}} \); \(b = \sqrt {{d^2} - {a^2}} \); \(a = \sqrt {{d^2} - {b^2}} \)
Với \(a = 8\); \(b = 6\) ta có: \(d = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10\)
Với \(a = \sqrt {15} \); \(d = \sqrt {24} \) ta có: \(b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}} = \sqrt {24 - 15} = \sqrt 9 = 3\)
Với \(b = 5\); \(d = 13\) ta có: \(a = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12\)
Vận dụng 1
Tìm bốn ví dụ về hình chữ nhật trong thực tế

Áp dụng định nghĩa hình chữ nhật và ứng dụng vào thực tiễn tìm các ví dụ về hình chữ nhật

Các ví dụ về hình chữ nhật trong thực tế: Mặt bảng; ti vi; mặt bàn; khung ảnh
Hoạt động 3
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
Advertisements (Quảng cáo)
a) Nếu \(\widehat {{\rm{BAD}}}\) là góc vuông thì \(\widehat {{\rm{ADC}}}\) và \(\widehat {{\rm{ABC}}}\) cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {{\rm{BAD}}}\) vuông.

Áp dụng tính chất của hình bình hành

a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\)
\(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\)
Nếu \(\widehat {{\rm{BAD}}} = 90^\circ \) suy ra \(AB \bot AD\)
Mà \(AB\) // \(CD\); \(AD\) // \(BC\)
Suy ra \(AD \bot CD;\;AB \bot BC\)
Suy ra \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
b) Xét \(\Delta BAD\) và \(\Delta CDA\) ta có:
\(BA = CD\) (gt)
\(AD\) chung
\(BD = AC\) (gt)
Suy ra \(\Delta BAD = \Delta CDA\) (c-c-c)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}\) (hai góc tương ứng)
Mà \(\widehat {BAD} + \widehat {CDA} = 180^\circ \)(do \(AB\) // \(CD\) , cặp góc trong cùng phía)
Suy ra \(\widehat {BAD} = \widehat {CDA} = 90^\circ \)
Thực hành 2
Chỉ được sử dụng compa, hãy kiểm tra tứ giác có phải là hình chữ nhật hay không.


Sử dụng compa đo độ dài các cạnh, đường chéo

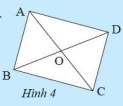
Gọi tứ giác trong hình là \(ABCD\)
Sử dụng compa đo độ dài ta thu được \(AB = CD\); \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) ta có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Hình bình hành \(ABCD\) có hai đường chéo \(AC = BD\) nên là hình chữ nhật
Vận dụng 2
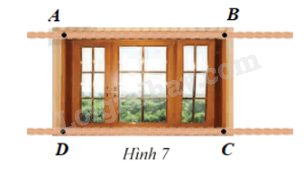
a) Hãy sử dụng ê ke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không?
b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không?


a) Sử dụng ê ke đo 3 góc của tứ giác rồi tinh góc còn lại
b) Đo độ dài các cạnh, đường chéo

a) Sử dụng ê ke, ta thấy khung cửa có 3 góc vuông
Áp dụng tính chất tổng 4 góc trong tứ giác, suy ra góc còn lại cũng là góc vuông
Vậy khung cửa là hình chữ nhật
b)
Sử dụng thước dây:
- Đo độ dài đoạn thẳng \(AB\) và đánh dấu 2 điểm trên đoạn dây (trùng với điểm \(A\), \(B\))
- Đặt một đầu đánh dấu trùng với điểm \(C\) và kiểm tra thấy điểm đánh dấu còn lại trùng với \(D\).
Vậy \(AB = CD\)
Thực hành tương tự ta có \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Mà \(AC = BD\) nên \(ABCD\) là hình chữ nhật
Vậy khung cửa có dạng hình chữ nhật
