Hoạt động 3
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .
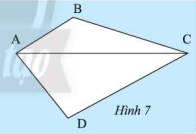

Sử dụng tính chất: Tổng ba góc trong một tam giác bằng \(180^\circ \)

Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
Thực hành 2
Tìm \(x\) trong mỗi tứ giác sau:
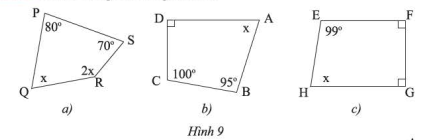

Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)

Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
a) Trong tứ giác \(PQRS\):
\(x + 2x = 360^\circ - \left( {80^\circ + 70^\circ } \right) = 210^\circ \)
\(3x = 210^\circ \)
Advertisements (Quảng cáo)
\(x = 70^\circ \)
b) Trong tứ giác \(ABCD\):
\(x = 360^\circ - \left( {90^\circ + 100^\circ + 95^\circ } \right)\)
\(x = 50^\circ \)
c) Trong tứ giác \(EFGH\):
\(x = 360^\circ - \left( {99^\circ + 90^\circ + 90^\circ } \right)\)
\(x = 81^\circ \)
Vận dụng 2
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.
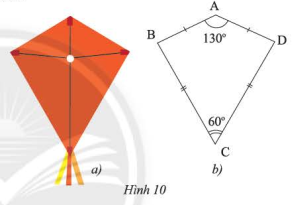

Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)

Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(130^\circ + \widehat B + 60^\circ + \widehat D = 360^\circ \)
\(\widehat B + \widehat D = 170^\circ \) (1)
Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = DC\) (gt)
\(AC\) chung
\( \Rightarrow \Delta ABC = \Delta ADC\) (c-c-c)
\( \Rightarrow \widehat B = \widehat D\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ \)
