
Tính thể tích của một hình chóp tam giác đều, biết chiều cao của hình chóp là 8 cm, bán kính đường tròn ngoại tiếp tam giác đáy bằng 12 cm.

Gọi I là tâm đường tròn ngoại tiếp ∆ABC đều
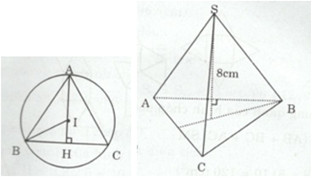
=> I là trọng tâm, trực tâm của ∆ABC
Gọi H là giao điểm của AI và BC
\( \Rightarrow AH \bot BC\) và \(AI = {2 \over 3}AH \)
Advertisements (Quảng cáo)
\(\Rightarrow AH = {{3AI} \over 2} = {{3.12} \over 2} = 18(cm) \)
\(\Rightarrow IH = AH - AI = 6(cm)\)
∆BHI vuông tại H nên \(BH = \sqrt {B{I^2} - I{H^2}} = \sqrt {{{12}^2} - {6^2}} \)\(\,= \sqrt {108} (cm)\)
\( \Rightarrow BC = 2BH = 2\sqrt {108} (cm)\)
Thể tích của hình chóp tam giác đều:
\(\eqalign{ & V = {1 \over 3}{S_{ABC}}.h = {1 \over 3}.{1 \over 2}AH.BC.h \cr & = {1 \over 3}.{1 \over 2}.18.2\sqrt {108} .8 = 48\sqrt {108} (c{m^3}) \cr} \)
