
Bác Lan muốn may một cái lều cắm trại bằng vải bạt cói dạng hình chóp tứ giác đều với kích thước đã cho trên hình. Em hãy cho biết:
a) Bác Lan phải dùng ít nhất bao nhiêu m2 vải bạt ?
b) Thể tích không khí trong lều sau khi làm xong ?
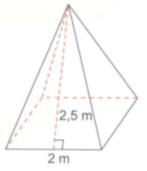

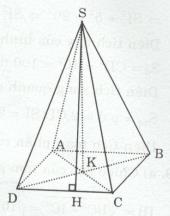
a) Diện tích xung quanh của hình chóp đều:
\({S_{xq}} = p.d = 2CD.SH = 2.2.2,5\)\(\, = 10(c{m^2})\)
Số vải bạt cần có để dựng lều chính là diện tích xung quanh của hình chóp đều
Vậy bác Lan phải dùng ít nhất 10m2 vải bạt
Advertisements (Quảng cáo)
b) ∆SCD cân tại S có SH là đường cao
=> SH là đường trung tuyến
=> H là trung điểm của CD
∆KDC vuông tại K có KH là đường trung tuyến (H là trung điểm của CD)
\( \Rightarrow KH = {{CD} \over 2}\) (đường trung tuyến ứng với cạnh huyền) => KH = 1 (m)
∆SHK vuông tại K có: \(S{K^2} + K{H^2} = S{H^2}\) (định lí Py-ta-go)
\( \Rightarrow S{K^2} + 1 = 2,{5^2} \Rightarrow S{K^2} = 5,25\)
\(\Rightarrow SK = \sqrt {5,25} (m)\)
Thể tích không khí trong lều sau khi làm xong:
\(V = {1 \over 3}{S_d}.h = {1 \over 3}.D{C^2}.SK \)\(\,= {1 \over 3}{.2^2}.\sqrt {5,25} = {{2\sqrt {21} } \over 3}({m^3})\)
