
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 40 cm, cạnh bên SA = 48 cm.
a) Tính chiều cao và thể tích của hình chóp.
b) Tính trung đoạn và diện tích toàn phần của hình chóp.

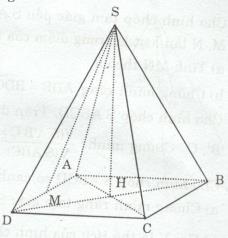
a) ABCD là đa giác đều => ABCD là hình vuông
∆ABC vuông tại B có:
\(A{C^2} = A{B^2} + B{C^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow A{C^2} = {6^2} + {6^2} = 72 \cr&\Rightarrow AC = 6\sqrt 2 (cm) \cr & \Rightarrow AH = {{6\sqrt 2 } \over 2} = 3\sqrt 2 (cm) \cr} \)
∆SAH vuông tại H có:
Advertisements (Quảng cáo)
\(S{H^2} + A{H^2} = S{A^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow S{H^2} + 18 = {48^2} \cr & \Rightarrow S{H^2} = 2286 \Rightarrow SH = 3\sqrt {254} (cm) \cr} \)
Thể tích của hình chóp: \(V = {1 \over 3}{S_d}.h = {1 \over 3}{.40^2}.3\sqrt {254}\)\(\, = 1600\sqrt {254} (c{m^3})\)
b) ∆SAD cân tại S có SM là đường trung tuyến
=> SM là đường cao \( \Rightarrow SM \bot AD\) tại M
Trung đoạn của hình chóp: \(d = SM = \sqrt {S{A^2} - A{M^2}} \)\(\, = \sqrt {{{48}^2} - {{20}^2}} = 4\sqrt {119} (cm)\)
Diện tích xung quanh của hình chóp:
\({S_{xq}} = p.d = 2AB.SM = 2.40.4\sqrt {119} \)\(\,= 320\sqrt {119} (c{m^2})\)
Diện tích toàn phần của hình chóp: \({S_{tp}} = {S_{xq}} + {S_d} \)\(\,= 320\sqrt {119} + {40^2} \approx 5090,79(c{m^2})\)
