
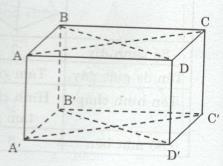
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 6 cm, AD = 8 cm và AA’ = 12 cm.
a) Chứng minh các tứ giác AA’C’C, BB’D’D là những hình chữ nhật.
b) Chứng minh rằng:
AC’2 = AB2 + AD2 + AA’2
Tính độ dài đoạn AC’.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.

a) Ta có: \(AA’ \bot (A’B’C’D’) \Rightarrow AA’ \bot A’C’\)
\(\Rightarrow \widehat {AA’C’} = 90^\circ \)
\(\eqalign{ & AA’ \bot (ABCD) \Rightarrow AA’ \bot AC\cr& \Rightarrow \widehat {A’AC} = 90^\circ \cr & (A’B’C’D’) \bot (CC’D’D) \cr&\Rightarrow CC’ \bot A’C’ \Rightarrow \widehat {CC’A’} = 90^\circ \cr} \)
Tứ giác AA’C’C có:
\(\widehat {AA’C} = 90^\circ ,\widehat {A’AC} = 90^\circ ,\)\(\,\widehat {CC’A’} = 90^\circ \)
=> AA’C’C là hình chữ nhật
\(\eqalign{ & BB’ \bot (A’B’C’D’) \Rightarrow BB’ \bot B’D’ \cr&\Rightarrow \widehat {BB’D’} = 90^\circ \cr & D{\rm{D’}} \bot {\rm{(A’B’C’D’)}} \Rightarrow {\rm{DD’}} \bot {\rm{B’D’}}\cr& \Rightarrow \widehat {DD’B’} = 90^\circ \cr & BB’ \bot (ABCD) \Rightarrow BB’ \bot BD\cr& \Rightarrow \widehat {B’BD} = 90^\circ \cr} \)
Tứ giác BB’D’D có:
\(\widehat {BB’D’} = 90^\circ ,\widehat {DD’B’} = 90^\circ ,\) \(\widehat {B’BD} = 90^\circ \)
Advertisements (Quảng cáo)
=> Tứ giác BB’D’D là hình chữ nhật
b) ∆ABD vuông tại A có \(A{B^2} + A{D^2} = B{D^2}\) (định lý Py-ta-go)
\( \Rightarrow A{B^2} + A{D^2} + AA{‘^2} = B{D^2} + AA{‘^2}\)
Mà AA’ = CC’ (AA’C’C là hình chữ nhật)
Và BD = AC (ABCD là hình chữ nhật)
\( \Rightarrow A{B^2} + A{D^2} + AA{‘^2} = A{C^2} + CC{‘^2}\)
Lại có \(A{C^2} + CC{‘^2} = AC{‘^2}\) (định lí Py-ta-go trong tam giác ACC’ vuông tại C)
Do đó \(A{B^2} + A{D^2} + AA{‘^2} = AC{‘^2}\)
\(AC{‘^2} = {6^2} + {8^2} + {12^2} = 244\)
\(\Rightarrow AC’ = 2\sqrt {61} (cm)\)
c) Thế tích của hình hộp chữ nhật: \(V = AB.AD.AA’ = 6.8.12 \)\(\,= 576(c{m^3})\)
Diện tích một mặt đáy của hình hộp chữ nhật: \({S_d} = 6.8 = 48(c{m^2})\)
Diện tích xung quanh của hình hộp chữ nhật:
\({S_{xq}} = 2p.h = 2(AB + AD).AA’\)\(\, = 2(6 + 8).12 \)\(\,= 336(c{m^2})\)
Diện tích toàn phần của hình hộp chữ nhật:
\({S_{tp}} = {S_{xq}} + {S_d}.2 = 336 + 48.2 \)\(\,= 432(c{m^2})\)
