Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông - Bài tập 7 trang 134 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Cho hình 61, trong đó ABCD là hình bình hành.
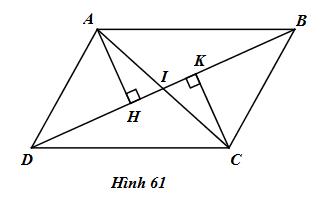
Cho hình 61, trong đó ABCD là hình bình hành.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi I là trung điểm của BD. Chứng minh rằng ba điểm A, I, C thẳng hàng.
a) Xét \(\Delta ADH\,\,\left( {\widehat H = {{90}^0}} \right)\) và \(\Delta KBC\,\,\left( {\widehat K = {{90}^0}} \right)\) có:
\(AD = BC\) (ABCD là hình bình hành)
Advertisements (Quảng cáo)
\(\widehat {ADH} = \widehat {KBC}\) (hai góc so le trong và \(AD // BC\))
Do đó \(\Delta ADH = \Delta CBK\) (cạnh huyền – góc nhọn)
\( \Rightarrow AH = CK\)
Mà AH // CK (cùng vuông góc với DB)
\( \Rightarrow \) Tứ giác AHCK là hình bình hành
b) Hình bình hành ABCD có I là trung điểm của BD nên I là trung điểm của AC
\( \Rightarrow A,I,C\) thẳng hàng.