
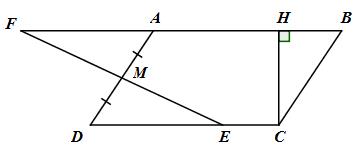
Cho hình bình hành ABCD có M là trung điểm của AD và E là một điểm tuỳ ý trên đoạn CD. Đường thẳng EM căt AB tại F. Hãy so sánh diện tích cùa hình bình hành ABCD và tứ giác ECBF.

Xét \(\Delta AMF\) và \(\Delta MED\) có:
\(MA = MD\) (M là trung điểm của AD)
\(\widehat {AMF} = \widehat {DME}\) (hai góc đối đỉnh)
\(\widehat {FAM} = \widehat {MDE}\) (hai góc so le trong và \(AF // DE\))
Do đó \(\Delta AMF = \Delta DME\,\left( {g.c.g} \right)\)
Advertisements (Quảng cáo)
Tứ giác ECBF có :
EC // BF (DC // AB, \(E \in CD,\,\,F \in BA\)) \( \Rightarrow \) Tứ giác ECBF là hình thang
Kẻ \(CH \bot AB\) tại H
\({S_{ECBF}} = {1 \over 2}CH\left( {EC + BF} \right) = {1 \over 2}CH\left( {EC + AF + AB} \right)\),
Mà \(AF = DE\,\,\left( {\Delta AMF = \Delta DME} \right)\)
Và \(AB = CD\) (ABCD là hình bình hành)
Nên \({S_{ECBF}} = {1 \over 2}CH\left( {EC + DE + CD} \right) = {1 \over 2}CH\left( {CD + CD} \right) = {1 \over 2}CH.2CD = CH.CD = {S_{ABCD}}\)
