
Ở hình 28, cho BN = 8 cm. Tính BC.
Trên hình 28, M là trung điểm của AD, N là trung điểm của BC. Đoạn thẳng MN gọi là đường trung bình của hình thang ABCD.
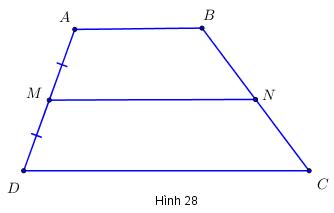

Dùng thước đo góc để đo các góc: \(\widehat A;\,\,\widehat D;\,\,\widehat {AMN}\) ta có: \(\widehat A = {110^0};\,\,\widehat D = {70^0};\,\,\widehat {AMN} = {70^0}\)
\(\widehat A + \widehat D = {110^0} + {70^0} = {180^0};\,\,\widehat A\) và \(\widehat D\) là hai góc trong cùng phía bù nhau.
Do đó AB // CD (dấu hiệu nhận biết hai đường thẳng song song)
Advertisements (Quảng cáo)
Suy ra tứ giác ABCD là hình thang.
\(\widehat {AMN} = \widehat D\,\,\left( { = {{70}^0}} \right);\,\,\widehat {AMN}\) và \(\widehat D\) là hai góc đồng vị.
Do đó MN // CD (dấu hiệu nhận biết hai đường thẳng song song) nên MN // AB
Hình thang ABCD (AB // CD) có M là trung điểm của AD, MN // AB, MN // CD
\( \Rightarrow N\) là trung điểm của BC \( \Rightarrow BN = {1 \over 2}BC \Rightarrow BC = 2BN\).
Mà \(BN = 8cm\,\,\left( {gt} \right)\)
Vậy \(BC = 2.8 = 16\,\,\left( {cm} \right)\).
