Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.. Bài 59 trang 92 sgk toán 8 tập 2 - Ôn tập chương III - Tam giác đồng dạng
Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.
Giải
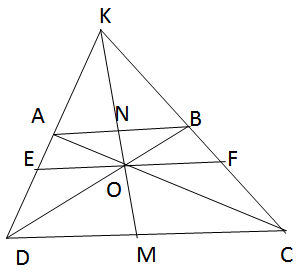
Qua O kẻ đường thẳng song song với AB, CD cắt AD, BC lần lượt tại E, F.
Ta có: OE = OF (xem cách chứng minh ở bài tập 20)
Do đó: \({{AN} \over {EO}} = {{KN} \over {KO}}\) (AN // EO)
Advertisements (Quảng cáo)
Mà \({{BN} \over {OF}} = {{KN} \over {KO}}\) (BN // OF)
=>\({{AN} \over {EO}} = {{BN} \over {FO}}\) Mà OE = OF
=>AN = BN hay N là trung điểm của AB.
Chứng minh tương tự: \({{DM} \over {OE}} = {{CM} \over {OF}} = > MD = MC\)
=>M là trung điểm của CD.
