Tam giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ một điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL (E thuộc BC, F thuộc AB). Các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự tại M, N
Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.
Giải:
(hình trang 125 sgbt)
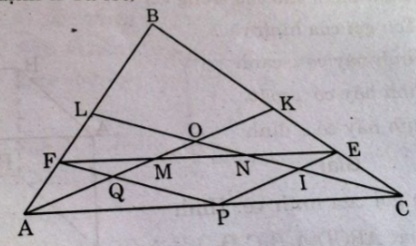
Gọi Q là giao điểm của PF và AK, I là giao điểm của PE và CL.
Trong tam giác FBE, ta có:
PE // AK hay QM // PE
Suy ra: \({{FQ} \over {FB}} = {{FM} \over {FE}}\) (Định lí Ta-lét ) (1)
Trong tam giác ALO, ta có:
PF // CL hay FQ // LO
Suy ra: \({{AF} \over {AL}} = {{FQ} \over {LO}}\) (Định lí Ta-lét ) (2)
Trong tam giác ALC,ta có:
PF // CL
Suy ra: \({{AF} \over {AL}} = {{FP} \over {CL}}\) (Định lí Ta-lét ) (3)
Từ (2) và (3) suy ra \({{FQ} \over {LO}} = {{FP} \over {CL}} \Rightarrow {{FQ} \over {FP}} = {{LO} \over {CL}}\)
Vì LO = \({1 \over 3}\) CL (tính chất đường trung tuyến) nên \({{FQ} \over {FP}} = {1 \over 3}\) (4)
Advertisements (Quảng cáo)
Từ (1) và (4) suy ra \({{FM} \over {FE}} = {1 \over 3} \Rightarrow FM = {1 \over 3}FE\)
Trong tam giác EBF, ta có:
PF // CL hay NI // PF
Suy ra: \({{EI} \over {EP}} = {{EN} \over {EF}}\) (Định lí Ta-lét ) (5)
Trong tam giác CKO, ta có: EI // OK
Suy ra: \({{CE} \over {CK}} = {{EI} \over {KO}}\) (Định lí Ta-lét ) (6)
Trong tam giác CKA, ta có: PE // AK
Suy ra: \({{CE} \over {CK}} = {{EP} \over {AK}}\) (Định lí Ta-lét ) (7)
Từ (6) và (7) suy ra :
\(\eqalign{ & {{EI} \over {OK}} = {{EP} \over {AK}} \cr & \Rightarrow {{EI} \over {EP}} = {{OK} \over {AK}} \cr} \)
Vì OK = \({1 \over 3}\)AK (tính chất đường trung tuyến) nên:
\({{EI} \over {EP}} = {1 \over 3}\) (8)
Từ (5) và (8) suy ra :
\(\eqalign{ & {{EN} \over {EF}} = {1 \over 3} \cr & \Rightarrow EN = {1 \over 3}EF \cr} \)
Ta có:
\(\eqalign{ & MN = EF - \left( {EN + FM} \right) \cr & = EF - \left( {{1 \over 3}EF + {1 \over 3}EF} \right) = {1 \over 3}EF \cr} \)
Vậy EN = MN = NF.
