Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.. Bài 7 trang 133 sgk toán 8 tập 2 - Phần Hình học - Ôn tập cuối năm - Toán 8
Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.
Hướng dẫn làm bài:
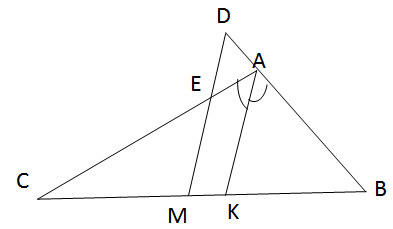
AK là đường phân giác của tam giác ABC nên
\({{KB} \over {AB}} = {{KC} \over {AC}}\) (1)
Vì MD // AK nên:
Advertisements (Quảng cáo)
∆ABK ∽ ∆DBM và ∆ECM ∽ ∆ACK
Do đó:
\({{KB} \over {AB}} = {{BM} \over {BD}}\) và \( {{CM} \over {CE}} = {{KC} \over {AC}}\) (2)
Từ (1) và (2) ta có: \({{BM} \over {BD}} = {{CM} \over {CE}}\) (3)
Do BM = CM (giả thiết) nên từ (3) suy ra : BD = CE
