Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB.

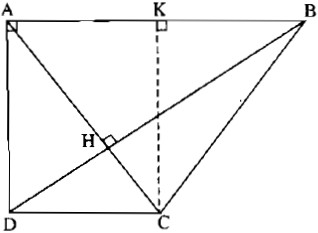
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
\({{HD} \over {HB}} = {{A{D^2}} \over {A{B^2}}} = {{{4^2}} \over {{6^2}}} = {4 \over 9}.\)
Advertisements (Quảng cáo)
Dễ thấy ∆HDC đồng dạng với ∆HBA nên
\({{DC} \over {AB}} = {{HD} \over {HB}} = {4 \over 9}\) suy ra \(DC = {4 \over 9}.6 = {8 \over 3}\left( {cm} \right)\)
Kẻ đường cao CK của tam giác ABC, dễ thấy \(KB = AB-DC = 6 - {8 \over 3} = {{10} \over 3}.\)
Từ đó \(B{C^2} = K{B^2} + K{C^2} = K{B^2} + A{D^2} = {{100} \over 9} + 16 = {{244} \over 9}\) suy ra \(BC = {{\sqrt {244} } \over 3} = {{2\sqrt {61} } \over 3}\left( {cm} \right)\)
Tam giác vuông ABD có \(D{B^2} = A{B^2} + A{D^2} = {6^2} + {4^2} = 52\), từ đó \(DB = \sqrt {52} = 2\sqrt {13} \left( {cm} \right)\)
