Cho tam giác ABC vuông cân tại A, đường trung tuyến BM. Gọi D là chân đường vuông góc kẻ từ C đến BM và H là chân đường vuông góc kẻ từ D đến AC. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ? Tại sao ? . Câu 1.9. Trang 106 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông cân tại A, đường trung tuyến BM. Gọi D là chân đường vuông góc kẻ từ C đến BM và H là chân đường vuông góc kẻ từ D đến AC. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ? Tại sao ?
a) ∆HCD đồng dạng với ∆ABM.
b) AH = 2HD.
Advertisements (Quảng cáo)
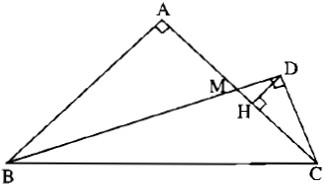
a) Hai tam giác vuông HCD và DCM đồng dạng ( có cùng góc nhọn tại C) mà ∆DCM đồng dạng với ∆ABM ( vì là hai tam giác vuông có \(\widehat {DMC} = \widehat {AMB}\), vậy ∆HCD đồng dạng với ∆ABM. Khẳng định a) đúng.
b) Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC ( H là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH ( do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.