Cho hai đoạn thẳng có độ dài là a và b. Dựng các đoạn thẳng có độ dài tương ứng bằng:
a) \(\sqrt {{a^2} + {b^2}}\) b) \(\sqrt {{a^2} - {b^2}} \,\,\left( {a > 0} \right)\)

a) \(\sqrt {{a^2} + {b^2}}\)
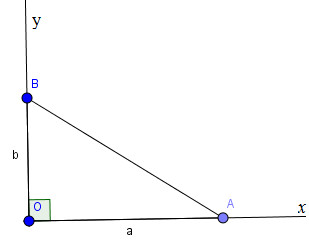
* Cách dựng (hình a):
− Dựng góc vuông xOy.
− Trên tia Ox, dựng đoạn OA = a.
− Trên tia Oy, dựng đoạn OB = b.
− Nối AB ta có đoạn \(AB = \sqrt {{a^2} + {b^2}} \) cần dựng.
* Chứng minh:
Áp dụng định lý Pi-ta-go vào tam giác vuông AOB, ta có:
\(A{B^2} = O{A^2} + O{B^2} = {a^2} + {b^2}\)
Advertisements (Quảng cáo)
Suy ra: \(AB = \sqrt {{a^2} + {b^2}} \)
b) \(\sqrt {{a^2} - {b^2}} \,\,\left( {a > 0} \right)\)
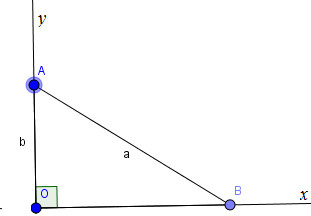
* Cách dựng (hình b):
− Dựng góc vuông xOy.
− Trên tia Ox, dựng đoạn OA = b.
− Dựng cung tròn tâm A, bán kính bằng a cắt Oy tại B.
Ta có đoạn \(OB = \sqrt {{a^2} - {b^2}} (a > b)\) cần dựng.
* Chứng minh;
Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
\(A{B^2} = O{A^2} + O{B^2} \Rightarrow O{B^2} = A{B^2} - O{A^2} = {a^2} - {b^2}\)
Suy ra: \(OB = \sqrt {{a^2} - {b^2}} \)
