Cho tam giác ABC vuông tại A. Câu 11. Trang 104 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông tại A. Biết rằng \({{AB} \over {AC}} = {5 \over 6}\), đường cao \(AH = 30cm\). Tính HB, HC.
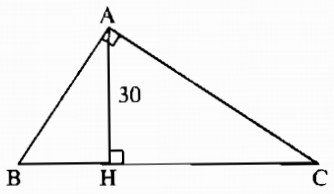
Xét hai tam giác vuông AHB và CHA, ta có:
\(\widehat {AHB} = \widehat {CHA} = {90^0}\)
\(\widehat {ABH} = \widehat {CAH}\) (hai góc cùng phụ \(\widehat {ACB}\))
Advertisements (Quảng cáo)
Vậy ∆AHB đồng dạng ∆CHA (g.g)
Suy ra: \({{AH} \over {HC}} = {{AB} \over {CA}}.\) (1)
Theo đề bài: \({{AB} \over {AC}} = {5 \over 6}\) và \(AH = 30(cm)\) (2)
Từ (1) và (2) suy ra: \({{30} \over {HC}} = {5 \over 6} \Rightarrow HC = {{30.6} \over 5} = 36(cm)\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(A{H^2} = HB.HC \Rightarrow HB = {{A{H^2}} \over {HC}} = {{{{30}^2}} \over {36}} = 25(cm)\)