Cho hình chữ nhật ABCD. Đường phân giác của góc B cắt đường chéo AC thành hai đoạn \(4{2 \over 7}m\) và \(5{5 \over 7}m\). Tính các kích thước của hình chữ nhật.

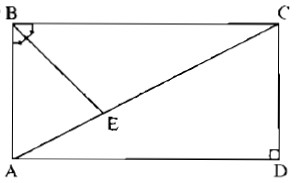
Trong tam giác ABC, gọi giao điểm đường phân giác của góc \(\widehat {ABC}\) với cạnh AC là E.
Theo đề bài ta có:
\(AE = 4{2 \over 7}m,\,EC = 5{5 \over 7}m.\)
Theo tính chất của đường phân giác, ta có: \({{AE} \over {EC}} = {{AB} \over {BC}}\)
Suy ra: \({{AB} \over {BC}} = {{4{2 \over 7}} \over {5{5 \over 7}}} = {{{{30} \over 7}} \over {{{40} \over 7}}} = {3 \over 4}\)
Suy ra: \({{AB} \over 3} = {{BC} \over 4} \Rightarrow {{A{B^2}} \over 9} = {{B{C^2}} \over {16}}\)
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC, ta có:
Advertisements (Quảng cáo)
\(A{C^2} = A{B^2} + B{C^2}\)
Mà \(AC = AE + EC\) nên:
\(\eqalign{
& A{B^2} + B{C^2} = {(AE + EC)^2} \cr
& = {\left( {4{2 \over 7} + 5{5 \over 7}} \right)^2} = {\left( {{{30} \over 7} + {{40} \over 7}} \right)^2} = {10^2} = 100 \cr} \)
Mà :
\(\eqalign{
& {{A{B^2}} \over 9} = {{B{C^2}} \over {16}} = {{A{B^2} + B{C^2}} \over {9 + 16}} \cr
& = {{A{B^2} + B{C^2}} \over {25}} = {{100} \over {25}} = 4 \cr} \)
Suy ra: \(A{B^2} = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\left( m \right)\)
\(B{C^2} = 16.4 = 64 \Rightarrow BC = \sqrt {64} = 8\left( m \right)\)
Vậy: \(AB = CD = 6m\)
\(BC = AD = 8m\)
