Cho tam giác ABC vuông tại A, vẽ đường cao AH. Chu vi của tam giác ABH là 30cm và chu vi của tam giác ACH là 40cm. Tính chu vi của tam giác ABC.

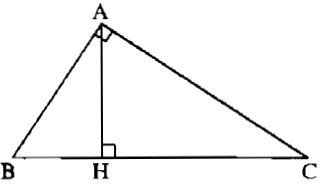
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: \(b = 30cm,c = 40cm.\)
Xét hai tam giác vuông AHB và CHA, ta có:
\(\widehat {AHB} = \widehat {CHA} = 90^\circ \)
\(\widehat {ABH} = \widehat {CAH}\) (hai góc cùng phụ \(\widehat {ACB}\))
Vậy \(\Delta AHB\) đồng dạng \(\Delta CHA\) (g.g)
Advertisements (Quảng cáo)
Suy ra: \({{HB} \over {HA}} = {{HA} \over {HC}} = {{BA} \over {AC}} = {{HB + HA + BA} \over {HA + HC + AC}} = {b \over c}\)
Suy ra: \({{BA} \over {AC}} = {b \over c} = {{30} \over {40}} = {3 \over 4}\)
Suy ra: \({{BA} \over 3} = {{AC} \over 4} \Rightarrow {{B{A^2}} \over 9} = {{A{C^2}} \over {16}} = {{B{A^2} + A{C^2}} \over {9 + 16}} = {{B{A^2} + A{C^2}} \over {25}}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
Suy ra: \({{B{A^2}} \over 9} = {{A{C^2}} \over {16}} = {{B{C^2}} \over {25}} \Rightarrow {{BA} \over 3} = {{AC} \over 4} = {{BC} \over 5}\)
Ta có các tam giác ABH, CAH, CBA đồng dạng với nhau nên:
\(b:c:a = BA:AC:BC = 3:4:5\)
Suy ra: \({b \over 3} = {c \over 4} = {a \over 5} \Leftrightarrow {{30} \over 3} = {{40} \over 4} = {a \over 5} \Rightarrow a = {{30} \over 3}.5 = 50\left( {cm} \right)\)
