Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kể MD, ME, MF lần lượt vuông góc với các cạnh BC, AC, AB. Chứng minh rằng:
\(B{D^2} + C{E^2} + A{F^2} = D{C^2} + E{A^2} + F{B^2}.\)
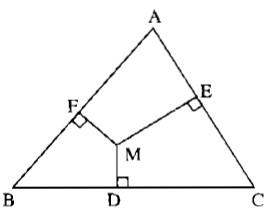

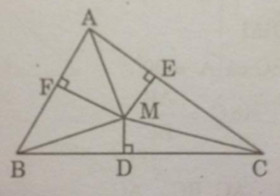
Áp dụng định lí Pi-ta-go vào tam giác vuông BDM, ta có:
\(B{M^2} = B{D^2} + D{M^2} \Rightarrow B{D^2} = B{M^2} - D{M^2}\) (1)
Áp dụng đinh lí Pi-ta-go vào tam giác vuông CEM, ta có:
\(C{M^2} = C{E^2} + E{M^2} \Rightarrow C{E^2} = C{M^2} - E{M^2}\) (2)
Áp dụng định lí pi-ta-go vào tam giác vuông AFM, ta có:
\(A{M^2}{\rm{ = A}}{{\rm{F}}^2} + F{M^2} \Rightarrow A{F^2} = A{M^2} - F{M^2}\) (3)
Cộng từng vế của (1), (2) và (3) ta có:
Advertisements (Quảng cáo)
\(B{D^2} + C{E^2} + A{F^2}\)
\(= B{M^2} - D{M^2} + C{M^2} - E{M^2} + A{M^2} - F{M^2}\) (4)
Áp dụng định lí Pi-ta-go vào tam giác vuông BFM, ta có:
\(B{M^2} = B{F^2} + F{M^2}\) (5)
Áp dụng định lí Pi-ta-go vào tam giác vuông CDM, ta có:
\(C{M^2} = C{D^2} + D{M^2}\) (6)
Áp dụng định lí Pi-ta-go vào tam giác vuông AEM, ta có:
\(A{M^2} = A{E^2} + E{M^2}\) (7)
Thay (5), (6), (7) vào (4) ta có:
\(\eqalign{
& B{D^2} + C{E^2}{\rm{ + A}}{{\rm{F}}^2} \cr
& = B{F^2} + F{M^2} - D{M^2} + C{D^2} + D{M^2} - E{M^2} + A{E^2} + E{M^2} - F{M^2} \cr
& = D{C^2} + E{A^2} + F{B^2} \cr} \)
Vậy \(B{D^2} + C{E^2}{\rm{ + A}}{{\rm{F}}^2} = D{C^2} + E{A^2} + F{B^2}.\)
