Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.

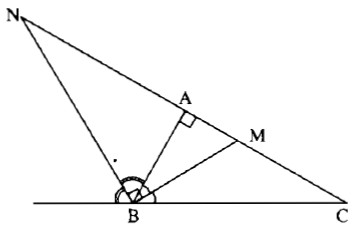
Vì BM là đường phân giác của góc B nên ta có:
\({{MA} \over {MC}} = {{AB} \over {BC}} \Rightarrow {{MA} \over {MA + MC}} = {{AB} \over {AB + BC}}\) (Tính chất tỉ lệ thức)
Advertisements (Quảng cáo)
Suy ra: \(MA = {{AB.(MA + MC)} \over {AB + BC}} = {{6.8} \over {6 + 10}} = {{48} \over {16}} = 3\left( {cm} \right)\)
Vì BN là đường phân giác của góc ngoài đỉnh B nên ta có: \(BM \bot BN\)
Suy ra tam giác BMN vuông tại B.
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: \(A{B^2} = AM.AN\)
Suy ra: \(AN = {{A{B^2}} \over {AM}} = {{{6^2}} \over 3} = {{36} \over 3} = 12\left( {cm} \right)\)
