Cho tam giác ABC. Chứng minh rằng. Câu 2.16. Trang 110 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 2. Tỉ số lượng giác của góc nhọn
Cho tam giác ABC có \(\widehat A = 60^\circ \). Chứng minh rằng:
BC2 = AB2 + AC2 – AB.AC.

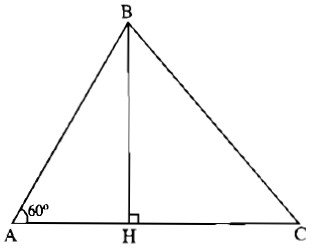
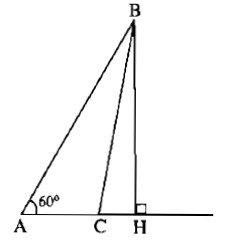
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để \(\widehat {BAC} = 60^\circ \) là góc nhọn ), do đó HC2 = (AC – AH)2
Công thức Py-ta-go cho ta:
Advertisements (Quảng cáo)
BC2 = BH2 + HC2
= BH2 + (AC – AH)2
= BH2 + AH2 +AC2 – 2AC.AH
= AB2 + AC2 – 2AC.AH.
Do \(\widehat {BAC} = 60^\circ \) nên AH = AB cos60º = \({{AB} \over 2},\) suy ra BC2 = AB2 + AC2 − AB.AC .
