Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng. Câu 2.17 Trang 110 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 2. Tỉ số lượng giác của góc nhọn
Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng:
\({S_{ABCD}} = {1 \over 2}AC.BD.\sin a.\)
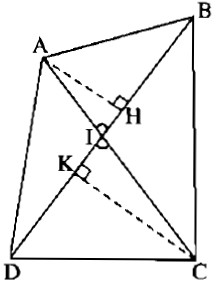
Giả sử hai đường chéo AC, BD cắt nhau tại I, \(\widehat {AIB} = \alpha \) là góc nhọn.
Advertisements (Quảng cáo)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AIsinα, CK = CIsinα, diện tích tam giác ABD là \({S_{ABD}} = {1 \over 2}BD.AH,\) diện tích tam giác CBD là: \({S_{CBD}} = {1 \over 2}BD.CK.\)
Từ đó diện tích S của tứ giác ABCD là:
\(\eqalign{
& S = {S_{ABD}} + {S_{CBD}} \cr
& = {1 \over 2}BD.(AH + CK) \cr
& = {1 \over 2}BD.(AI + CI)\sin \alpha \cr
& = {1 \over 2}{\rm{BC}}{\rm{.ACs}}in\alpha \cr} \)