Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C (O), D (O’)).
a) Chứng minh rằng khi cát tuyến quay xung quang điểm A thì \(\widehat {CBD}\) có số đo không đổi.
b) Từ C và D vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A.
Giải
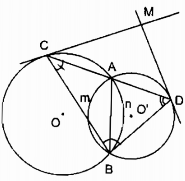
a) Trong ∆ABC ta có:
sđ \(\overparen{AnB}\)
sđ \(\overparen{AmB}\)
Vì có A, B cố định nên sđ \(\overparen{AnB}\), sđ \(\overparen{AmB}\) không thay đổi nên \(\widehat C,\widehat D\) có số đo không đổi
Advertisements (Quảng cáo)
\(\widehat {CBD} = {180^0} - \left( {\widehat C + \widehat D} \right)\) không đổi
Vậy cát tuyến CAD thay đổi số đo \(\widehat {CBD}\) không đổi.
b) Trong (O) ta có
\(\widehat {ABC} = \widehat {MCA}\) (hệ quả góc giữa tia tiếp tuyến và dây) (1)
Trong (O’) ta có: \(\widehat {ABD} = \widehat {MDA}\) (hệ quả góc giữa tia tiếp tuyến và dây) (2)
Từ (1) và (2) suy ra: \(\widehat {MCA} + \widehat {MDA} = \widehat {ABC} + \widehat {ABD} = \widehat {CBD}\)
Hay \(\widehat {MCD} + \widehat {MDC} = \widehat {CBD}\) (không đổi)
Trong ∆MCD ta có: \(\widehat {CMD} = {180^0} - \left( {\widehat {MCD} + \widehat {MDC}} \right)\)
= \({180^0} - \widehat {CBD}\) (không đổi)
