Từ một điểm M cố định ở bên ngoài đường tròn tâm O ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh rằng ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB.
b) Ở hình 2 khi cho MB = 20 cm, MB = 50 cm, tính bán kính đường tròn.
Giải
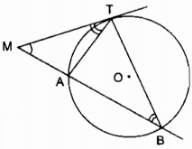
a) Xét ∆MTA và ∆MTB:
Có góc \(\widehat M\) chung
\(\widehat {MTA} = \widehat {TBA}\) (hệ quả góc giữa tia tiếp tuyến và dây)
Hay \(\widehat {MTA} = \widehat {TBM}\)
Suy ra: ∆MAT đồng dạng ∆MTB
Advertisements (Quảng cáo)
\({{MT} \over {MA}} = {{MB} \over {MT}}\)
\( \Rightarrow M{T^2} = MA.MB\)
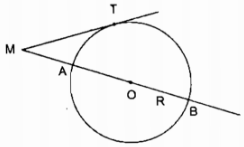
b) Gọi bán kính (O) là R
MB = MA + AB = MA + 2R
\( \Rightarrow MA = MB - 2R\)
\(M{T^2} = MA.MB\) (chứng minh trên)
\( \Rightarrow M{T^2} = \left( {MB - 2R} \right)MB\)
\( \Rightarrow R = {{M{B^2} - M{T^2}} \over {2MB}}\)
\( = {{2500 - 400} \over {2.50}}\) = 21 (cm)
