Cho các hàm số :
\(y = 2x - 2\); (d1)
\(y = - {4 \over 3}x - 2\); (d2)
\(y = {1 \over 3}x + 3\). (d3)
a) Vẽ đồ thị của các hàm số đã cho trên cùng một mặt phẳng tọa độ .
b) Gọi giao điểm của đường thẳng (d3) với (d1) và (d2) theo thứ tự là A, B. Tìm tọa độ của A, B
c) Tính khoảng cách AB.

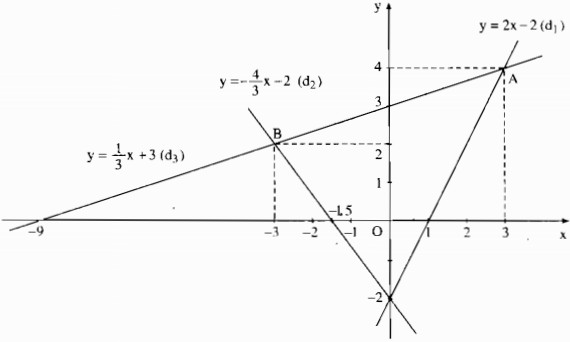
a) *Vẽ đồ thị hàm số y = 2x -2 (d1)
Cho x = 0 thì y = - 2 . Ta có :
Cho y = 0 thì 2x – 2 = 0 \( \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\). Ta có: (1; 0)
Đồ thị hàm số đi qua hai điểm (0; 2) và (1; 0)
*Vẽ đồ thị hàm số \(y = - {4 \over 3}x - 2\) (d2)
Cho x = 0 thì y = -2. Ta có:
Cho y = 0 thì \( - {4 \over 3}x - 2 = 0 \Leftrightarrow x = - 1,5\) . Ta có: \(\left( { - 1,5;0} \right)\)
Advertisements (Quảng cáo)
Đồ thị hàm số đi qua hai điểm \(\left( {0; - 2} \right)\) và \(\left( { - 1,5;0} \right)\)
* Vẽ đồ thị hàm số \(y = {1 \over 3}x + 3\) (d3)
Cho x = 0 thì y = 3. Ta có: (0;3)
Cho y = 0 thì \({1 \over 3}x + 3 = 0 \Leftrightarrow x = - 9\). Ta có: (-9; 0)
Đồ thị hàm số đi qua hai điểm (0; 3) và (-9; 0)
b) Phương trình hoành độ giao điểm của (d1) và (d3) :
\(\eqalign{
& 2x - 2 = {1 \over 3}x + 3 \cr
& \Leftrightarrow 2x - {1 \over 3}x = 3 + 2 \cr
& \Leftrightarrow {5 \over 3}x = 5 \Leftrightarrow x = 3 \cr} \)
Tung độ giao điểm: \(y = 2.3 - 2 \Leftrightarrow y = 6 - 2 = 4\)
Vậy tọa độ điểm A là : A(3; 4)
Phương trình hoành độ giao điểm của (d2) và (d3):
\(\eqalign{
& - {4 \over 3}x - 2 = {1 \over 3}x + 3 \cr
& \Leftrightarrow {1 \over 3}x + {4 \over 3}x = - 2 - 3 \cr
& \Leftrightarrow {5 \over 3}x = - 5 \Leftrightarrow x = - 3 \cr} \)
Tung độ giao điểm :
\(y = {1 \over 3}.\left( { - 3} \right) + 3 \Leftrightarrow y = - 1 + 3 = 2\)
Vậy tọa độ điểm B là : A(-3 ; 2)
c) Ta có:
\(\eqalign{
& A{B^2} = {\left( {{x_A} - {x_B}} \right)^2} + {\left( {{y_A} - {y_B}} \right)^2} \cr
& = {\left( {3 + 3} \right)^2} + {\left( {4 - 2} \right)^2} = 40 \cr
& AB = \sqrt {40} = 2\sqrt {10} \cr} \).
