
Cho tam giác ABC vuông tại A ( AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.
a) Xét vị trí tương đối của đường tròn (O) và (O’).
b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.
c) Chứng minh rằng EF là tiếp tuyến chung của đường tròn (O) và (O’).
d) Trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.
a) Hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O’;R’} \right)\) tiếp xúc ngoài với nhau \( \Leftrightarrow R + R’ = OO’\).
b) Chứng minh tứ giác \(AEHF\) có 3 góc vuông.
c) Chứng minh \(EF \bot OE\) và \(EF \bot OF\).
d) Chứng minh tam giác \(ANF\) vuông tại N, áp dụng hệ thức lượng trong tam giác vuông và định lí Pytago trong tam giác vuông tính AN và NF.

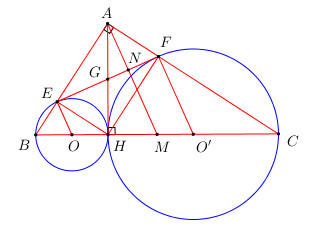
a) Gọi O và O’ lần lượt là trung điểm của BH và CH \( \Rightarrow O\) và \(O’\) lần lượt là tâm đường tròn đường kính BH và đường tròn đường kính CH.
Ta có \(OH + O’H = OO’ \Rightarrow \left( O \right)\) và \(\left( {O’} \right)\) tiếp xúc ngoại tại \(H\).
b) Do \(E\) thuộc đường tròn đường kính \(BH\) nên \(\angle BEH = {90^0} \Rightarrow \angle AEH = {90^0}\).
Do \(F\) thuộc đường tròn đường kính \(CH\) nên \(\angle CFH = {90^0} \Rightarrow \angle AFH = {90^0}\).
Xét tứ giác \(AEHF\) có \(\angle EAF = \angle AEH = \angle AFH = {90^0} \Rightarrow \) Tứ gíac \(AEHF\) là hình chữ nhật (Tứ giác có 3 góc vuông).
c) Gọi \(G = AH \cap EF\). Do \(AEHF\) là hình chữ nhật nên \(GA = GE = GH = GF\).
Ta có \(\Delta GHE\) cân tại \(G \Rightarrow \angle GEH = \angle GHE\).
\(\Delta OHE\) cân tại \(O \Rightarrow \angle OEH = \angle OHE\)
\( \Rightarrow \angle GEH + \angle OEH = \angle GHE + \angle OHE\)
\(\Rightarrow \angle OEG = \angle OHG = {90^0}\)
Advertisements (Quảng cáo)
\( \Rightarrow EF \bot OE\), mà \(OE\) là bán kính của \(\left( O \right)\).
\( \Rightarrow EF\) là tiếp tuyến của \(\left( O \right)\).
Hoàn toàn tương tự ta chứng minh được \(EF \bot OF\), mà \(OF\) là bán kính của \(\left( {O’} \right)\).
\( \Rightarrow EF\) là tiếp tuyến của \(\left( {O’} \right)\).
Vậy \(EF\) là tiếp tuyến chung của \(\left( O \right)\) và \(\left( {O’} \right)\).
d) Do \(AM\) là đường trung tuyến của tam giác vuông \(ABC \) \(\Rightarrow AM = \dfrac{1}{2}BC = MC \) \(\Rightarrow \Delta MAC\) cân tại \(M \Rightarrow \angle MAC = \angle MCA\).
Lại có \(\angle MCA = \angle O’CF = \angle O’FC\) (do tam giác \(O’FC\) cân tại \(O’\))
\( \Rightarrow \angle MAC = \angle O’FC\).
Mà 2 góc này ở vị trí 2 góc đồng vị \( \Rightarrow AM//O’F\). Lại có \(O’F \bot EF\,\,\left( {cmt} \right) \Rightarrow AM \bot EF\) tại \(N\).
\( \Rightarrow \Delta ANF\) vuông tại \(N\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\)
\(\Rightarrow BC = 10\) (cm).
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có \(AH.BC = AB.AC\)
\(\Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{6.8}}{{10}} = 4,8\,\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông ABH ta có
\(\begin{array}{l}A{H^2} = AE.AB\\ \Rightarrow AE = \dfrac{{A{H^2}}}{{AB}} = \dfrac{{4,{8^2}}}{6} = 3,84\,\,\left( {cm} \right)\\ \Rightarrow HE = \sqrt {A{H^2} - A{E^2}}\\\;\;\;\;\;\; = \sqrt {4,{8^2} - 3,{{84}^2}} = 2,88\,\,\left( {cm} \right) \\\;\;\;\;\;\;= AF\end{array}\).
Áp dụng hệ thức lượng trong tam giác vuông AEF ta có:
\(\dfrac{1}{{A{N^2}}} = \dfrac{1}{{A{E^2}}} + \dfrac{1}{{A{F^2}}} \)\(\,= \dfrac{1}{{3,{{84}^2}}} + \dfrac{1}{{2,{{88}^2}}}\)
\(\Rightarrow AN = 2,304\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông ANF có:
\(NF = \sqrt {A{F^2} - A{N^2}} \)\(\,= \sqrt {2,{{88}^2} - 2,{{304}^2}} = 1,728\,\,\left( {cm} \right)\).
Vậy \({S_{ANF}} = \dfrac{1}{2}AN.NF \)\(\, = \dfrac{1}{2}.2,304.1,728 = 1,990656\,\,\left( {c{m^2}} \right)\).
Baitapsgk.com
