
Từ điểm A ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC với đường tròn ( B, C là hai tiếp điểm). Kẻ đường kính CD của (O).
a) Chứng minh rằng BD//AO.
b) AD cắt đường tròn (O) tại E (A, E, D theo thứ tự). Chứng minh rằng \(A{B^2} = AE.AD\).
c) Vẽ \(BH \bot DC\) tại H. Gọi I là trung điểm của BH. Chứng minh rằng ba điểm A, I, D thẳng hàng.

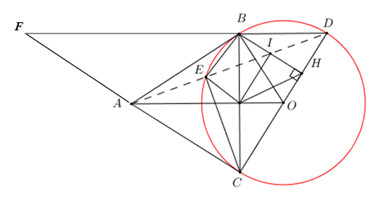
a) Ta có : \(AB = AC\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của \(BC\).
\(OB = OC = R \Rightarrow O\) thuộc trung trực của \(BC\) .
\( \Rightarrow OA\) là trung trực của \(BC \Rightarrow OA \bot BC\).
Có \(B\)thuộc đường tròn đường kính \(CD \Rightarrow \Delta BCD\)vuông tại \(B \Rightarrow BD \bot BC\).
\( \Rightarrow BD//AO\) (từ vuông góc đến song song).
b) Do \(E\) thuộc đường tròn đường kính \(CD \Rightarrow \Delta ECD\) vuông tại \(E \Rightarrow CE \bot AD\).
Xét \(\Delta ACE\) và \(\Delta ADC\) có:
\(\begin{array}{l}\angle CAD\,\,chung;\\\angle AEC = \angle ACD = {90^0}\end{array}\)
Advertisements (Quảng cáo)
\( \Rightarrow \Delta ACE \sim \Delta ADC\,\,\left( {g.g} \right)\)
\(\Rightarrow \dfrac{{AC}}{{AD}} = \dfrac{{AE}}{{AC}}\) \( \Rightarrow A{C^2} = AE.AD\).
Mà \(AB = AC\,\,\left( {cmt} \right) \Rightarrow A{B^2} = AE.AD\).
c) Kéo dài BD cắt AC tại F.
Ta có : \(OA \bot BC;\,\,BD \bot BC\) \( \Rightarrow OA//BD\) hay \(OA//DF\).
Xét tam giác CDF có :
O là trung điểm của BD ;
\(OA//DF\) ;
\( \Rightarrow A\) là trung điểm của \(FC \Rightarrow AC = AF\) (tính chất đường trung bình của tam giác).
Ta có : \(\left\{ \begin{array}{l}BH \bot AD\,\,\left( {gt} \right)\\AC \bot AD\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BH//AC\).
Gọi \(I’ = AD \cap GH\).
Áp dụng định lí Ta –lét ta có : \(\dfrac{{BI’}}{{AF}} = \dfrac{{DI’}}{{DA}} = \dfrac{{I’H}}{{AC}}\).
Mà \(AF = AC\,\,\left( {cmt} \right) \Rightarrow I’\) là trung điểm của \(BH \Rightarrow I’ \equiv I\).
Vậy \(A,I,D\) thẳng hàng.
Baitapsgk.com
