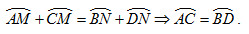Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Xét 2 TH tâm O nằm ngoài hai dây song song và tâm O nằm trong hai dây song song. Chứng minh cung AM = cung BN và cung CM = cung DN .

TH1: Tâm O nằm ngoài hai dây song song.
Kẻ đường kính MN // AB // CD.
Ta có: \(\widehat A = \widehat {AOM};\,\,\widehat B = \widehat {BON}\) (các góc so le trong bằng nhau).
Advertisements (Quảng cáo)
Mà \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \widehat A = \widehat B\)
\( \Rightarrow \widehat {AOM} = \widehat {BON} \Rightarrow cung\,AM = cung\,BN\)
Chứng minh hoàn toàn tương tự ta có cung CM = cung DN
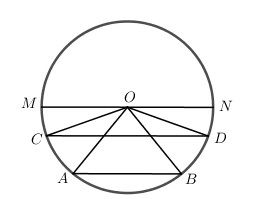
Vì C, D lần lượt nằm trên cung AM và BN nên ta có 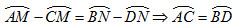 .
.

TH2 : Tâm O nằm trong hai dây song song.
Kẻ đường kính MN // AB // CD.
Chứng minh hoàn toàn tương tự ta có: 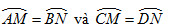
Vì M, D lần lượt nằm trên cung AM và BN nên ta có :