Bài 2 trang 129 Tài liệu dạy – học Toán 9 tập 1: Cho đường tròn tâm O, bán kính 50cm....

Cho đường tròn tâm O, bán kính 50cm. Hai dây MN và PQ song song với nhau và có độ dài theo thứ tự là 80 cm và 96 cm. Tính khoảng cách giữa hai dây ấy.

Xét 2 trường hợp :

TH1: MN và PQ khác phía so với O.

TH2: MN và PQ nằm cùng phía so với O.

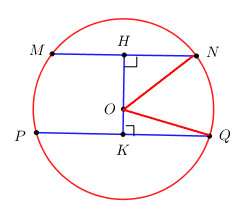
TH1: MN và PQ khác phía so với O.

Kẻ $OH \bot MN\,\,\left( {H \in MN} \right),$$\,\,OK \bot PQ\,\,\left( {K \in PQ} \right)$.

Áp dụng quan hệ vuông góc giữa đường kính và dây cung ta có H, K lần lượt là trung điểm của MN và PQ.

$\begin{array}{l} \Rightarrow HN = \dfrac{1}{2}MN = \dfrac{1}{2}.80 = 40\,\,\left( {cm} \right)\\\,\,\,\,\,\,KQ = \dfrac{1}{2}PQ = \dfrac{1}{2}.96 = 48\,\,\left( {cm} \right)\end{array}$

Áp dụng định lí Pytago trong tam giác vuông OHN có:

$O{H^2} = O{N^2} - H{N^2} = {50^2} - {40^2} = 900\\ \Rightarrow OH = \sqrt {900}  = 30\,\,\left( {cm} \right)$

Áp dụng định lí Pytago trong tam giác vuông OKQ có:

$O{K^2} = O{Q^2} - K{Q^2} = {50^2} - {48^2} = 196\\ \Leftrightarrow OK = \sqrt {196}  = 14\,\,\left( {cm} \right)$

Vì O nằm giữa H và K nên $HK = OH + OK = 30 + 14 = 44\,\,\left( {cm} \right)$

Vậy khoảng cách giữa hai dây MN và PQ là 44cm.

TH2: MN và PQ nằm cùng phía so với O.

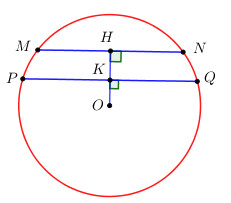
Kẻ $OH \bot MN\,\,\left( {H \in MN} \right),$$\,\,OK \bot PQ\,\,\left( {K \in PQ} \right)$.

Áp dụng quan hệ vuông góc giữa đường kính và dây cung ta có H, K lần lượt là trung điểm của MN và PQ.

$\begin{array}{l} \Rightarrow HN = \dfrac{1}{2}MN = \dfrac{1}{2}.80 = 40\,\,\left( {cm} \right)\\\,\,\,\,\,\,KQ = \dfrac{1}{2}PQ = \dfrac{1}{2}.96 = 48\,\,\left( {cm} \right)\end{array}$

Áp dụng định lí Pytago trong tam giác vuông OHN có:

$O{H^2} = O{N^2} - H{N^2} = {50^2} - {40^2} = 900\\ \Rightarrow OH = \sqrt {900}  = 30\,\,\left( {cm} \right)$

Áp dụng định lí Pytago trong tam giác vuông OKQ có:

$O{K^2} = O{Q^2} - K{Q^2} = {50^2} - {48^2} = 196\\ \Leftrightarrow OK = \sqrt {196}  = 14\,\,\left( {cm} \right)$

Vì K nằm giữa O và H nên $HK = OH - OK = 30 - 14 = 16\,\,\left( {cm} \right)$

Vậy khoảng cách giữa hai dây MN và PQ là 16cm.

 Baitapsgk.com