
Cho tứ giác ABCD có \(\widehat B = \widehat D = {90^o}\).
a) Chứng minh 4 điểm A, B, C, D cùng nằm trên cùng một đường tròn.
b) So sánh độ dài AC và BD.
+) Sử dụng định lí đường trung tuyến trong tam giác vuông.
+) Mọi dây không đi qua tâm đều nhỏ hơn đường kính.
Advertisements (Quảng cáo)

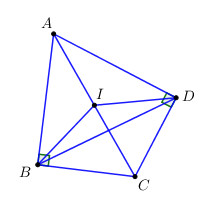
Gọi \(I\) là trung điểm của \(AC\).
Xét tam giác vuông AHC có \(IB = \dfrac{1}{2}AC = IA = IC\,\,\left( 1 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Xét tam giác vuông ADC có \(ID = \dfrac{1}{2}AC = IA = IC\,\,\left( 1 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).
Từ (1) và (2) \( \Rightarrow IB = ID = IA = IC \Rightarrow \) 4 điểm \(A,\,\,B,\,\,C,\,\,D\) cùng thuộc đường tròn tâm \(I\) đường kính \(AC\).
Xét đường tròn \(\left( {I;\dfrac{{AC}}{2}} \right)\) ta có \(AC\) là đường kính, \(BD\) là dây cung không đi qua tâm.
Vậy \(BD < AC\).
Baitapsgk.com
