
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với \(\widehat A = {60^o}\). Gọi H là giao điểm của các đường cao BB’ và CC’. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
+) Góc ở tâm gấp đôi góc nội tiếp cùng chắn 1 cung, tính \(\widehat {BOC}\).
+) Dựa vào tổng 4 góc trong tứ giác tính \(\widehat {B’HC’}\), tính \(\widehat {BHC}\).
+) Dựa vào tổng 3 góc trong tam giác IBC tính \(\widehat {BIC}\).
+) Chứng minh \(\widehat {BHC} = \widehat {BIC} = \widehat {BOC} = {120^0}\).

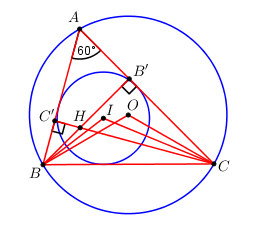
+) Góc \(\widehat {BAC}\) nội tiếp đường tròn \(\left( O \right)\) chắn cung .
Advertisements (Quảng cáo)
(góc ở tâm bằng số đo cung bị chắn).
+) Xét tứ giác AB’HC’ có:
\(\,\,\,\,\,\,\widehat {B’AC’} + \widehat {AB’H} + \widehat {AC’H} + \widehat {B’HC’} = {360^0}\) (tổng bốn góc của tứ giác).
\(\begin{array}{l} \Rightarrow {60^0} + {90^0} + {90^0} + \widehat {B’HC’} = {360^0}\\ \Rightarrow \widehat {B’HC’} = {120^0}\end{array}\)
Mà \(\widehat {B’HC’} = \widehat {BHC}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {BHC} = {120^0}\).
+) Vì I là tâm đường tròn nội tiếp tam giác ABC \( \Rightarrow BI;CI\) lần lượt là phân giác của \(\widehat {ABC};\,\,\widehat {ACB}\)
Xét tam giác IBC có:
\(\widehat {IBC} + \widehat {ICB} + \widehat {BIC} = {180^0}\) (tổng ba góc trong tam giác)
\(\begin{array}{l} \Rightarrow \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} + \widehat {BIC} = {180^0}\\ \Rightarrow \widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\\ \Rightarrow \widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right)\\ \Rightarrow \widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - {{60}^0}} \right)\\ \Rightarrow \widehat {BIC} = {180^0} - \dfrac{1}{2}{.120^0} = {120^0}\end{array}\)
Vậy \(\widehat {BHC} = \widehat {BIC} = \widehat {BOC} = {120^0} \Rightarrow H;I;O\) cùng nhìn BC dưới 1 góc 1200.
Vậy 5 điểm B, C, O, H, I cùng thuộc một đường tròn chứa góc 1200 dựng trên đoạn thẳng BC.
