
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I.
Chứng minh \(\widehat {AOC} = \widehat {AIC}\)
+) Góc ở tâm bằng số đo cung bị chắn.
+) Góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Hai cung nằm giữa hai dây song song thì bằng nhau.
Advertisements (Quảng cáo)

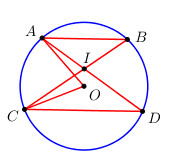
Vì \(\widehat {AOC}\) là góc ở tâm chắn cung AC nên \(\widehat {AOC} = sd\,cung\,AC\).
Vì \(\widehat {AIC}\) là góc có đỉnh ở bên trong đường tròn nên \(\widehat {AIC} = \dfrac{{sd\,cung\,AC + sd\,cung\,BD}}{2}\)
Do AB // CD nên cung AC = cung BC (hai cung nằm giữa hai dây song song thì bằng nhau).
\( \Rightarrow sdcung\,AC = sd\,cung\,BC \Rightarrow \widehat {AIC} = \dfrac{{sdcung\,AC + sd\,cung\,AC}}{2} = \dfrac{{2sdcung\,AC}}{2} = sdcung\,AC\)
Vậy \(\widehat {AOC} = \widehat {AIC}\).
