
Cho tam giác ABC nội tiếp đường tròn O với hai đường cao BE, CF cắt nhau tại H.
a) Chứng minh \(AH \bot BC\)
b) Tia AH cắt BC tại D. Chứng minh AF.AB = AH.AD = AE.AC
c) Chứng minh EB là tia phân giác của góc FED.
a) Chứng minh H là trực tâm tam giác ABC.
b) Chứng minh \(\Delta AFH \sim \Delta ADB\,\,\left( {g.g} \right);\,\,\Delta AHE \sim \Delta ACD\,\,\left( {g.g} \right)\).
c) Chứng minh 4 điểm B, E, F, C cùng thuộc đường tròn đường kính BC \( \Rightarrow \widehat {BEF} = \widehat {BCF}\).
Chứng minh 4 điểm H, E, C, D cùng thuộc đường tròn đường kính CH \( \Rightarrow \widehat {HED} = \widehat {BCF}\).
Từ đó suy ra \(\widehat {BEF} = \widehat {HED}\).

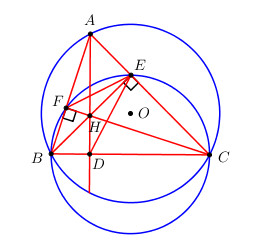
a) H là giao điểm hai đường cao BE và CF của tam giác ABC \( \Rightarrow H\) là trực tâm tam giác ABC.
Advertisements (Quảng cáo)
\( \Rightarrow AH \bot BC\).
b) Xét \(\Delta AHF\) và \(\Delta ABH\) có:
\(\widehat {AFH} = \widehat {ADB} = {90^0}\);
\(\widehat {BAD}\) chung;
\( \Rightarrow \Delta AFH \sim \Delta ADB\,\,\left( {g.g} \right) \Rightarrow \frac{{AF}}{{AD}} = \frac{{AH}}{{AB}} \Rightarrow AF.AB = AH.AD\,\,\left( 1 \right)\).
Xét \(\Delta AHE\) và \(\Delta ACD\) có:
\(\widehat {AEH} = \widehat {ADC} = {90^0};\)
\(\widehat {CAD}\) chung;
\( \Rightarrow \Delta AHE \sim \Delta ACD\,\,\left( {g.g} \right) \Rightarrow \frac{{AH}}{{AC}} = \frac{{AE}}{{AD}} \Rightarrow AH.AD = AE.AC\,\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow AF.AB = AH.AD = AE.AC\).
c) Ta có \(\widehat {BFC} = \widehat {BEC} = {90^0} \Rightarrow E;F\) thuộc đường tròn đường kính BC.
Xét đường tròn đường kính BC có: \(\widehat {BEF} = \widehat {BCF}\) (hai góc nội tiếp cùng chắn cung BF) (1).
Ta cũng có: \(\widehat {HDC} = \widehat {HEC} = {90^0} \Rightarrow \) D, E cùng thuộc đường tròn đường kính CH.
Xét đường tròn đường kính CH có: \(\widehat {HED} = \widehat {BCF}\) (hai góc nội tiếp cùng chắn cung HD) (2).
Từ (1) và (2) \( \Rightarrow \widehat {BEF} = \widehat {HED}\,\,\left( { = \widehat {BCF}} \right) \Rightarrow EB\)là tia phân giác của \(\widehat {FED}\).
