
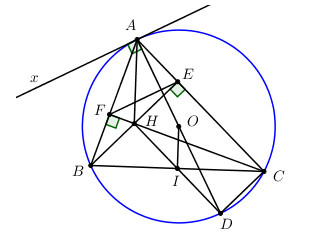
Cho tam giác ABC nhọn nội tiếp (O; R) có đường cao BE, CF cắt nhau tại H.
a) Chứng minh tứ giác BFEC nội tiếp.
b) Chứng minh \(OA \bot EF\) .
c) Kẻ đường kính AD của (O), BC cắt HD tại I. Chứng minh \(OI \bot BC\).
d) Giả sử \(BC = R\sqrt 3 \). Tính bán kính đường tròn ngoại tiếp tam giác AEF theo R.
a) Chứng minh 2 điểm E, F cùng thuộc đường tròn đường kính BC.
b) Kẻ tiếp tuyến Ax, chứng minh Ax//EF.
c) Chứng minh BDCH là hình bình hành, suy ra I là trung điểm của BC. Sử dụng quan hệ vuông góc giữa đường kính và dây cung.
d) Chứng minh tứ giác AEHF là tứ giác nội tiếp, suy ra bán kính đường tròn ngoại tiếp tam giác AEF. Sử dụng tính chất đường trung bình của tam giác và định lí Pytago tính bán kính đường tròn ngoại tiếp tam giác AEF.

a) Ta có \(\widehat {BEC} = \widehat {BFC} = {90^0} \Rightarrow \) 2 điểm E, F cùng nhìn BC dưới 1 góc 900 nên 2 điểm E, F cùng thuộc đường tròn đường kính BC \( \Rightarrow \) BCEF là tứ giác nội tiếp đường tròn đường kính BC tâm M.
b) Dựng tiếp tuyến Ax.
Advertisements (Quảng cáo)
Ta có: \(\widehat {ACB} = \widehat {BAx}\)(1) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB).
Tứ giác BCEF là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ACB} + \widehat {EFB} = {180^0}\) (Tổng 2 góc đối của tứ giác nội tiếp). Mà \(\widehat {EFB} + \widehat {AFE} = {180^0}\) (2 góc kề bù) \( \Rightarrow \widehat {ACB} = \widehat {AFE}\) (2).
Từ (1) và (2) \( \Rightarrow \widehat {BAx} = \widehat {AFE}\). Mà 2 góc này ở vị trí so le trong \( \Rightarrow Ax//EF\).
Mà \(OA \bot Ax\) (Do Ax là tiếp tuyến của đường tròn tại A).
Vậy \(OA \bot EF\).
c) Ta có \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CD \bot AC\). Mà \(BH \bot AC \Rightarrow BH//CD\).
Chứng minh tương tự ta có: CH//BD
Suy ra tứ giác BDCH là hình bình hành (Tứ giác có các cặp cạnh đối song song).
\( \Rightarrow \) Hai đường chéo BC và HD cắt nhau tại trung điểm mỗi đường.
\( \Rightarrow I\) là trung điểm của BC và HD.
Do đó \(OI \bot BC\) (quan hệ vuông góc giữa đường kính và dây cung).
d) Ta có \(\widehat {AEH} = \widehat {AFH} = {90^0}\,\,\left( {gt} \right) \Rightarrow E;F\) thuộc đường tròn đường kính AH. Do đó tứ giác AEHF nội tiếp đường tròn đường kính AH.
\( \Rightarrow \) Đường tròn ngoại tiếp tam giác AEF là đường tròn đường kính AH, có bán kính bằng \(\dfrac{{AH}}{2}\).
Ta có: OI là đường trung bình của tam giác AHD \( \Rightarrow OI = \dfrac{1}{2}AH\).
Xét tam giác vuông OIB có: \(OI = \sqrt {O{B^2} - I{B^2}} = \sqrt {{R^2} - {{\left( {\dfrac{{R\sqrt 3 }}{2}} \right)}^2}} = \sqrt {\dfrac{{{R^2}}}{4}} = \dfrac{R}{2}\).
Vậy bán kính đường tròn ngoại tiếp tam giác AEF bằng \(\dfrac{{AH}}{2} = \dfrac{R}{2}\).
