
Hãy vẽ các hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O ; R) rồi tính cạnh của các hình đó theo R.
Áp dụng định lí Pytago tính các cạnh của các hình.

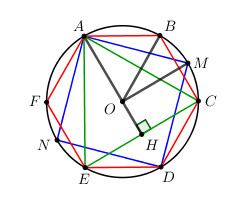
+) ABCDEF là lục giác đều \( \Rightarrow \widehat {AOB} = \dfrac{{{{360}^0}}}{6} = {60^0}\).
Xét tam giác OAB có : \(\left\{ \begin{array}{l}OA = OB = R\\\widehat {AOB} = {60^0}\end{array} \right. \Rightarrow \Delta OAB\) đều \( \Rightarrow AB = R\).
Vậy cạnh hình lục giác đều nội tiếp đường tròn \(\left( {O;R} \right)\)là R.
Advertisements (Quảng cáo)
+) AMDN là hình vuông \( \Rightarrow \widehat {AOM} = {90^0} \Rightarrow \Delta OAM\) vuông tại O
\( \Rightarrow O{A^2} + O{M^2} = A{M^2}\) (định lí Pytago)
\({R^2} + {R^2} = A{M^2} \Rightarrow A{M^2} = 2{R^2} \Leftrightarrow AM = R\sqrt 2 \).
Vậy cạnh hình vuông nội tiếp đường tròn \(\left( {O;R} \right)\)là \(R\sqrt 2 \).
+) ACE là tam giác đều. Gọi H là trung điểm của CE \( \Rightarrow AH \bot CE\) (đường trung tuyến đồng thời là đường cao).
O là tâm đường tròn ngoại tiếp tam giác đều ACE \( \Rightarrow O\) là trọng tâm tam giác ACE \( \Rightarrow AO = \dfrac{2}{3}AH \Rightarrow AH = \dfrac{3}{2}R\).
Xét tam giác vuông ACH có:\(A{H^2} + H{C^2} = A{C^2} \Leftrightarrow \dfrac{{9{R^2}}}{4} + {\left( {\dfrac{{AC}}{2}} \right)^2} = A{C^2}\)
\( \Leftrightarrow \dfrac{{9{R^2}}}{4} + \dfrac{{A{C^2}}}{4} = A{C^2} \Leftrightarrow \dfrac{{9{R^2}}}{4} = \dfrac{{3A{C^2}}}{4} \Leftrightarrow A{C^2} = 3{R^2} \Leftrightarrow AC = R\sqrt 3 \).
Vậy cạnh tam giác đều nội tiếp đường tròn \(\left( {O;R} \right)\)là \(R\sqrt 3 \).
