
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung sao cho sđ , sđ và sđ
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
a) Gọi E, F lần lượt là trung điểm của AB và CD, chúng minh \(OE \bot AB;\,\,OF \bot CD\) và \(E;O;F\) thẳng hàng, từ đó suy ra AB//CD.
Chứng minh \( \Rightarrow \widehat {ADC} = \widehat {BCD}\) suy ra ABCD là hình thang cân.
b) Sử dụng công thức tính số đo góc có đỉnh ở bên trong đường tròn.
c) Chứng minh tam giác OAB đều, tính AB.
Sử dụng định lí Pytago tính BC, suy ra AD.
Sử dụng công thức: Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền nhân sin góc đối tính CF, suy ra CD.

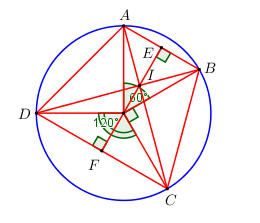
Gọi E, F lần lượt là trung điểm của AB và CD
\( \Rightarrow OE \bot AB;\,\,OF \bot CD\) (quan hệ vuông góc giữa đường kính và dây cung).
Advertisements (Quảng cáo)
Xét tam giác OAB có \(OA = OB \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow OE\) là phân giác của \(\widehat {AOB} \Rightarrow \widehat {BOE} = \dfrac{{{{60}^0}}}{2} = {30^0}\)
Tương tự ta có \(\widehat {COF} = \dfrac{1}{2}\widehat {COD} = {60^0}\)
\( \Rightarrow \widehat {EOF} = \widehat {BOE} + \widehat {BOC} + \widehat {COF} = {30^0} + {90^0} = {60^0} = {180^0}\)
\( \Rightarrow E;O;F\) thẳng hàng \( \Rightarrow EF \bot AB;\,\,EF \bot CD \Rightarrow AB//CD\)\( \Rightarrow ABCD\) là hình thang.
=>Cung AD = cung BC(hai cung giữa hai dây song song bằng nhau)
\( \Rightarrow cung\,AD + cung\,AB = cung\,BC + cung\,AB \Rightarrow cung\,BD = cung\,AC\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Vậy ABCD là hình thang cân (Hình thang có 2 góc ở đáy bằng nhau).
b) Gọi \(I = AC \cap BD \Rightarrow \widehat {BIC}\) là góc ở đỉnh ở bên trong đường tròn.
\( \Rightarrow \widehat {BIC} = \dfrac{{sdcung\,BC + sdcung\,AD}}{2} = \dfrac{{2sdcung\,BC}}{2} = sdcung\,BC = \widehat {BOC} = {90^0}\).
Vậy \(AC \bot BD\) tại I.
c) Xét tam giác OAB có : \(\left\{ \begin{array}{l}OA = OB = R\\\widehat {AOB} = {60^0}\end{array} \right. \Rightarrow \Delta OAB\) đều \( \Rightarrow AB = R\).
Xét tam giác vuông OBC có: \(O{B^2} + O{C^2} = B{C^2}\) (định lí Pytago)
\( \Rightarrow {R^2} + {R^2} = B{C^2} \Leftrightarrow B{C^2} = 2{R^2} \Rightarrow BC = R\sqrt 2 = AD\).
Xét tam giác vuông OCF có: \(CF = OC.\sin \widehat {COF} = R.\sin {60^0} = \dfrac{{R\sqrt 3 }}{2}\)
\( \Rightarrow CD = 2CF = 2\dfrac{{R\sqrt 3 }}{2} = R\sqrt 3 \).
