Bài tập - Chủ đề 1: Đo góc và cung - Bài 3 trang 79 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Cho hai đường tròn đồng tâm
Cho hai đường tròn đồng tâm \(\left( {O;R} \right)\); \(\left( {O;r} \right)\)với (R > r). Lấy điểm M ở ngoài hai đường tròn, qua M vẽ hai tiếp tuyến với \(\left( {O;r} \right)\), chúng lần lượt cắt \(\left( {O;R} \right)\)tại A, B và C, D. Chứng minh cung AB = cung CD
Sử dụng các tính chất:
+) Hai dây cách đều tâm thì bằng nhau.
+) Hai dây bằng nhau căng hai cung bằng nhau.
Advertisements (Quảng cáo)
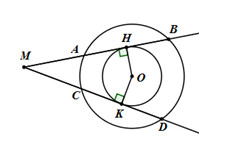
Gọi H, K lần lượt là các tiếp điểm của tiếp tuyến kẻ từ M đối với đường tròn \(\left( {O;r} \right)\) ta có \(OH = OK = r\)
\( \Rightarrow AB = CD\) (hai dây cách đều tâm thì bằng nhau)
cung AB = cung CD (hai dây bằng nhau căng hai cung bằng nhau).