
a) Vẽ đồ thị các hàm số y = -x và y = 2x + 3 trên cùng một mặt phẳng tọa độ.
b) Tìm giao điểm A của hai đường thẳng trong câu a. Tìm giao điểm B của đường thẳng \(y = 2x + 3\) với trục tung.
c) Tính diện tích tam giác AOB.
Đồ thị hàm số đi qua điểm \(A\left( {m;n} \right)\) nên ta thay \(x = m;y = n\) vào hàm số đã cho ta tìm được b.
Cách vẽ đồ thị hàm số bậc nhất \(y = ax + b,\,\,\left( {a \ne 0} \right)\)
Tìm tọa độ giao điểm của đồ thị hàm số \(y = ax + b\)với trục tung là \(A\left( {0;b} \right)\) và trục hoành \(B\left( { - \dfrac{b}{a};0} \right)\) .
Đồ thị hàm số cần tìm là đường thẳng đi qua 2 điểm A, B

a)
Bảng giá trị:
|
x |
0 |
- 1 |
|
Advertisements (Quảng cáo) y = -x |
0 |
1 |
|
y = 2x + 3 |
3 |
1 |
Đồ thị hàm số y = -x là đường thẳng đi qua 2 điểm có tọa độ \(\left( {0;0} \right);\left( { - 1;1} \right).\)
Đồ thị hàm số y = 2x + 3 là đường thẳng đi qua 2 điểm có tọa độ \(\left( {0;3} \right);\left( { - 1;1} \right).\)
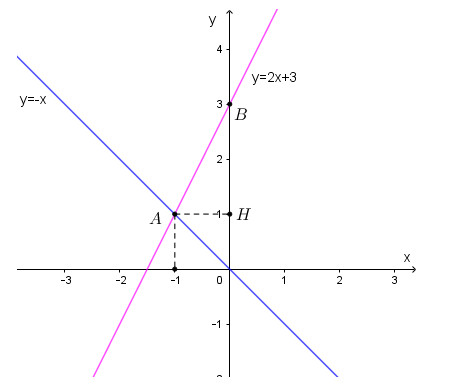
b) Dựa vào đồ thị ta thấy tọa độ giao điểm của 2 đường thẳng y = -x và y = 2x + 3 là \(A\left( { - 1;1} \right)\)
Đường thẳng \(y = 2x + 3\) giao với trục tung khi x = 0 nên y = 3. Khi đó ta có B(0;3)
c) Tính diện tích tam giác AOB.
Gọi H là chân đường cao kẻ từ A. Ta có: \(AH = \left| 1 \right| = 1;OB = \left| 3 \right| = 3\)
\({S_{OAB}} = \dfrac{1}{2}AH.OB = \dfrac{1}{2}.1.3 = \dfrac{3}{2}\)
