
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và \(\widehat {DCB} = \dfrac{1}{2}\widehat {ACB}\).
a) Chứng minh ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn ngoại tiếp tứ giác ABDC.
a) Chứng minh \(\widehat {DCB} = \widehat {BAD}\), từ đó suy ra tứ giác ABDC là tứ giác nội tiếp.
b) Chứng minh \(\widehat {ACB} = {90^0}\), sử dụng định lí góc nội tiếp chắn nửa đường tròn là góc vuông.

Advertisements (Quảng cáo)
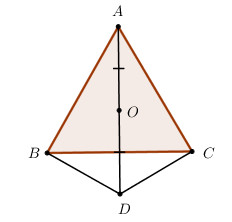
a) \(AB = AC\,\,\left( {gt} \right) \Rightarrow A\) thuộc trung trực của BC.
\(DB = DC\,\,\left( {gt} \right) \Rightarrow D\) thuộc trung trực của BC
\( \Rightarrow AD\) là trung trực của BC. Lại có tam giác ABC đều \( \Rightarrow AD\) đồng thời là phân giác của \(\widehat {BAC} \Rightarrow \widehat {BAD} = \dfrac{1}{2}\widehat {BAC} = \dfrac{1}{2}{.60^0} = {30^0}\).
Mà \(\widehat {DCB} = \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}{.60^0} = {30^0} \Rightarrow \widehat {DCB} = \widehat {BAD}\)
Vậy tứ giác ABDC là tứ giác nội tiếp (Tứ giác có 2 đỉnh cùng nhìn 1 cạnh dưới góc bằng nhau).
b) Ta có : \(\widehat {ACD} = \widehat {ACB} + \widehat {DCB} = {60^0} + {30^0} = {90^0} \Rightarrow \widehat {ACB}\) nội tiếp chắn nửa đường tròn \( \Rightarrow AD\) là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
Gọi O là trung điểm của AD. Vậy O là tâm đường tròn ngoại tiếp ABDC.
