
Từ một điểm M nằm ngoài đường tròn (O ; R) vẽ hai tiếp tuyến tiếp xúc với đường tròn A, B. Biết OM = 2R.
a) Tính độ dài cung nhỏ cung AB
b) Tính diện tích giới hạn bởi hai đoạn MA, MB và cung nhỏ AB.
a) Gọi C là trung điểm của OM, chứng minh tam giác OAC đều, tính \(\widehat {AOC}\) và suy ra số đo góc AOB.
Sử dụng công thức \(l = \dfrac{{\pi Rn}}{{180}}\).
b) Tính diện tích tứ giác OAMB và diện tích hình quạt OAB, từ đó suy ra diện tích hình cần tính.

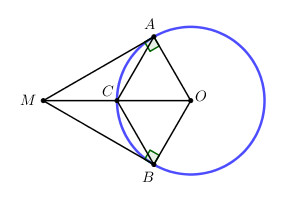
a) Gọi C là trung điểm của OM \( \Rightarrow OC = R \Rightarrow C \in \left( O \right)\).
Advertisements (Quảng cáo)
Xét tam giác vuông OAM có: \(AC = \dfrac{1}{2}OM = R\) (trung tuyến ứng với cạnh huyền trong tam giác vuông).
Xét tam giác OAC có: \(OA = OC = AC = R \Rightarrow \Delta OAC\) đều \( \Rightarrow \widehat {AOC} = {60^0}\).
Mà OM là tia phân giác của \(\widehat {AOB}\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {AOB} = 2\widehat {AOC} = {120^0}\).
b) Áp dụng định lí Pytago trong tam giác vuông OAM có:
\(AM = \sqrt {O{M^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \)
\( \Rightarrow AM = BM = R\sqrt 3 \) (tính chất 2 tiếp tuyến cắt nhau)
\(\begin{array}{l} \Rightarrow {S_{\Delta OAM}} = \dfrac{1}{2}OM.AM = \dfrac{1}{2}.R.R\sqrt 3 = \dfrac{{{R^2}\sqrt 3 }}{2}\\\,\,\,\,\,\,{S_{\Delta OBM}} = \dfrac{1}{2}OM.BM = \dfrac{1}{2}.R.R\sqrt 3 = \dfrac{{{R^2}\sqrt 3 }}{2}\\ \Rightarrow {S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = \dfrac{{{R^2}\sqrt 3 }}{2} + \dfrac{{{R^2}\sqrt 3 }}{2} = \dfrac{{2{R^2}\sqrt 3 }}{2} = {R^2}\sqrt 3 \end{array}\)
Diện tích hình quạt OAB là \({S_q} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {R^2}.120}}{{360}} = \dfrac{{\pi {R^2}}}{3}\)
Vậy diện tích giới hạn bởi hai đoạn MA, MB và cung nhỏ AB là:
\(S = {S_{OAMB}} - {S_q} = {R^2}\sqrt 3 - \dfrac{{\pi {R^2}}}{3} = {R^2}\left( {\sqrt 3 - \dfrac{\pi }{3}} \right)\).
