
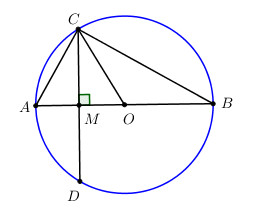
Cho đường tròn (O) đường kính AB. Lấy điểm M trên đoạn AO, vẽ dây CD vuông góc với AB tại M. Biết AM = 1 cm, CD = \(2\sqrt 3 \) cm. Tính:
a) Chu vi đường tròn.
b) Độ dài cung cung CAD .
a) Chứng minh tam giác ABC vuông tại C, áp dụng hệ thức lượng trong tam giác vuông, tính BM, từ đó tính AB và suy ra bán kính đường tròn \(\left( O \right)\).
Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\).
b) Tính \(\sin \widehat {COA} \Rightarrow \) số đo góc COA. Sử dụng công thức \(l = \dfrac{{\pi Rn}}{{180}}\) tính độ dài cung AC.
Chứng minh cung có độ dài gấp đôi cung AC.

Advertisements (Quảng cáo)
a) Vì \(AB \bot CD\) tại M \( \Rightarrow M\) là trung điểm của CD (Quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow CM = \dfrac{1}{2}CD = \sqrt 3 \).
Ta có: \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại C.
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
\(C{M^2} = AM.BM \Leftrightarrow BM = \dfrac{{C{M^2}}}{{AM}} = \dfrac{3}{1} = 3\) (cm)
\( \Rightarrow AB = AM + BM = 1 + 3 = 4\) (cm)
\( \Rightarrow \) Bán kính của đường tròn \(\left( O \right)\) là \(R = OA = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2\) (cm)
Vậy chu vi của đường tròn \(\left( O \right)\) là: \(C = 2\pi R = 2\pi .2 = 4\pi \,\,\left( {cm} \right)\).
b) \(\Delta ABC\) vuông tại C \( \Rightarrow CO = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2\,\,\left( {cm} \right)\) (định lí trung tuyến ứng với cạnh huyền trong tam giác vuông).
Xét tam giác vuông OCM có: \(\sin \widehat {COM} = \dfrac{{CM}}{{CO}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {COM} = {60^0} \Rightarrow \widehat {COA} = {60^0}\)
(cm).
Vì A thuộc trung trực của CD \( \Rightarrow AC = AD\) (điểm thuộc trung trực của đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó) \( \Rightarrow cung\,AC = cung\,AD \Rightarrow {l_{cungCAD}} = 2{l_{cungAC}} = \dfrac{{4\pi }}{3} \approx 4,19\,\,\left( {cm} \right)\).
