
Xét sự tương đương của các cặp hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x - y = - 1\\x - y = 2\end{array} \right.\) và \(\left\{ \begin{array}{l}x + 2y = - 2\\2x + 4y = 1\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x + y = - 3\\2x + 2y = - 6\end{array} \right.\) và \(\left\{ \begin{array}{l}x - 2y = 1\\2x - 4y = 2\end{array} \right.\)
c) \(\left\{ \begin{array}{l}x - y = 0\\x + y = 2\end{array} \right.\) và \(\left\{ \begin{array}{l}x + 2y = 3\\2x + y = 3\end{array} \right.\)
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

a)
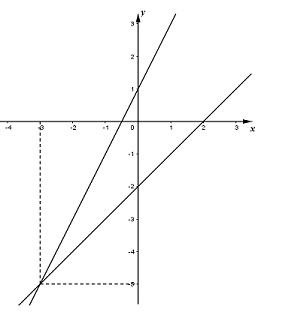
Hai đường thẳng \(2x - y = - 1\) và \(x - y = 2\) cắt nhau tại điểm có tọa độ \(\left( { - 3; - 5} \right) \Rightarrow \) Hệ phương trình \(\left\{ \begin{array}{l}2x - y = - 1\\x - y = 2\end{array} \right.\) có nghiệm \(\left( {x;y} \right) = \left( { - 3; - 5} \right)\).
\(x + 2y = - 2 \Leftrightarrow 2y = - x - 2 \Leftrightarrow y = \dfrac{{ - 1}}{2}x - 1\,\,\left( {{d_1}} \right);\,\,2x + 4y = 1 \Leftrightarrow 4y = - 2x + 1 \Leftrightarrow y = \dfrac{{ - 1}}{2}x + \dfrac{1}{4}\,\,\left( {{d_2}} \right)\)
Hai đường thẳng \(\left( {{d_1}} \right)//\left( {{d_2}} \right) \Rightarrow \) Hai đường thẳng này không cắt nhau, do đó hệ phương trình \(\left\{ \begin{array}{l}x + 2y = - 2\\2x + 4y = 1\end{array} \right.\) vô nghiệm.
Vậy hai hệ phương trình \(\left\{ \begin{array}{l}2x - y = - 1\\x - y = 2\end{array} \right.\) và \(\left\{ \begin{array}{l}x + 2y = - 2\\2x + 4y = 1\end{array} \right.\) không tương đương.
Advertisements (Quảng cáo)
b) \(\left\{ \begin{array}{l}x + y = - 3\\2x + 2y = - 6\end{array} \right.\) và \(\left\{ \begin{array}{l}x - 2y = 1\\2x - 4y = 2\end{array} \right.\)
\(x + y = - 3 \Rightarrow y = - x - 3\,\,\left( {{d_1}} \right);\,\,2x + 2y = - 6 \Leftrightarrow x + y = - 3 \Leftrightarrow y = - x - 3\,\,\left( {{d_2}} \right)\)
Ta có : \(\left( {{d_1}} \right) \equiv \left( {{d_2}} \right) \Rightarrow \) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại vô số điểm. Do đó hệ \(\left\{ \begin{array}{l}x + y = - 3\\2x + 2y = - 6\end{array} \right.\) vô số nghiệm.
\(x - 2y = 1 \Leftrightarrow 2y = x - 1 \Leftrightarrow y = \dfrac{1}{2}x - \dfrac{1}{2}\,\,\left( {{d_3}} \right);\,\,2x - 4y = 2 \Leftrightarrow x - 2y = 1 \Leftrightarrow 2y = x - 1 \Leftrightarrow y = \dfrac{1}{2}x - \dfrac{1}{2}\,\,\left( {{d_4}} \right)\)
Ta có : \(\left( {{d_3}} \right) \equiv \left( {{d_4}} \right) \Rightarrow \)Hai đường thẳng \(\left( {{d_3}} \right)\) và \(\left( {{d_4}} \right)\) cắt nhau tại vô số điểm. Do đó hệ \(\left\{ \begin{array}{l}x - 2y = 1\\2x - 4y = 2\end{array} \right.\) vô số nghiệm.
Vậy hai hệ phương trình \(\left\{ \begin{array}{l}x + y = - 3\\2x + 2y = - 6\end{array} \right.\) và \(\left\{ \begin{array}{l}x - 2y = 1\\2x - 4y = 2\end{array} \right.\) tương đương.
c) \(\left\{ \begin{array}{l}x - y = 0\\x + y = 2\end{array} \right.\) và \(\left\{ \begin{array}{l}x + 2y = 3\\2x + y = 3\end{array} \right.\)
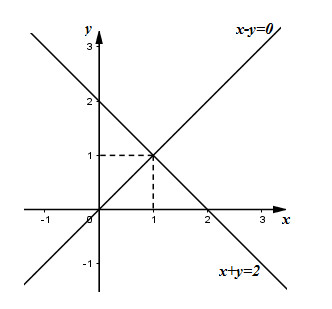
\(x - y = 0 \Leftrightarrow y = x\,\,\left( {{d_1}} \right);\,\,x + y = 2 \Leftrightarrow y = - x + 2\,\,\left( {{d_2}} \right)\)
Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại điểm có tọa độ \(\left( {1;1} \right) \Rightarrow \) Hệ phương trình \(\left\{ \begin{array}{l}x - y = 0\\x + y = 2\end{array} \right.\) có nghiệm \(\left( {x;y} \right) = \left( {1;1} \right)\).
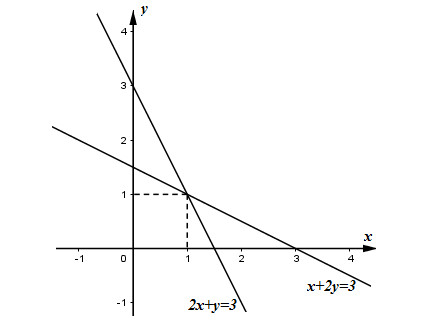
\(x + 2y = 3 \Leftrightarrow 2y = - x + 3 \Leftrightarrow y = \dfrac{{ - 1}}{2}x + \dfrac{3}{2}\,\,\left( {{d_3}} \right);\,\,2x + y = 3 \Leftrightarrow y = - 2x + 3\,\,\left( {{d_4}} \right)\)
Hai đường thẳng \(\left( {{d_3}} \right)\) và \(\left( {{d_4}} \right)\) cắt nhau tại điểm có tọa độ \(\left( {1;1} \right)\) nên hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 3\\2x + y = 3\end{array} \right.\) có nghiệm \(\left( {x;y} \right) = \left( {1;1} \right)\).
Vậy hai hệ phương trình \(\left\{ \begin{array}{l}x - y = 0\\x + y = 2\end{array} \right.\) và \(\left\{ \begin{array}{l}x + 2y = 3\\2x + y = 3\end{array} \right.\) tương đương.
