
Cho tam giác ABC vuông tại A có diện tích \(37,5c{m^2},AB < AC\), đường cao AH có độ dài 6 cm. Tính các độ dài AB, AC.
Áp các cách tính diện tích và định lý Pythagore trong tam giác vuông để tìm ra hai mối quan hệ giữa AB, AC, từ đó rút thế để giải.

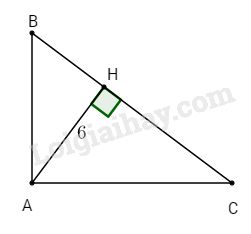
Có \({S_{\Delta ABC}} = \dfrac{{AB.AC}}{2} \)
Advertisements (Quảng cáo)
\(\Rightarrow AB.AC = 2.{S_{\Delta ABC}} = 2.37,5 = 75\\ \Rightarrow AB = \dfrac{{75}}{{AC}}\)
Mặt khác: \({S_{\Delta ABC}} = \dfrac{{AH.BC}}{2}\)
\(\Rightarrow BC = \dfrac{{2.{S_{\Delta ABC}}}}{{AH}} = \dfrac{{2.37,5}}{6} = \dfrac{{25}}{2}\) (cm)
Áp dụng định lý Pythagore trong tam giác ABC vuông tại A:
\(A{B^2} + A{C^2} = B{C^2} \\\Rightarrow \dfrac{{{{75}^2}}}{{A{C^2}}} + A{C^2} = {\left( {\dfrac{{25}}{2}} \right)^2}\\ \Leftrightarrow {75^2} + A{C^4} = {\left( {\dfrac{{25}}{2}} \right)^2}.A{C^2}\)
\( \Leftrightarrow \left[ \begin{array}{l}A{C^2} = 100\\A{C^2} = \dfrac{{225}}{4}\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}AC = 10 \Rightarrow AB = \dfrac{{15}}{2}\\AC = \dfrac{{15}}{2} \Rightarrow AB = 10\end{array} \right.\,\,\)
Mà \(AB < AC \Rightarrow AC = 10;\,\,AB = \dfrac{{15}}{2}\)
